Er zijn 170 resultaten gevonden
- 13 jul 2020, 09:50
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Benaderen van een (klein) logaritme
- Reacties: 2
- Weergaves: 7878
Re: Benaderen van een (klein) logaritme
Het heeft dan geen zin om je bovengrens te vergroten: Klopt, ik deed dat vooral omdat ik weet wat \frac{\sqrt 2}{2} is, maar ik heb niks om te staven dat dat ook daadwerkelijk groter is dan \ln 2 . Ik probeer juist een beetje van die logs uit af te komen en jouw oplossing is een leuke, dank je! Nat...
- 12 jul 2020, 13:11
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Benaderen van een (klein) logaritme
- Reacties: 2
- Weergaves: 7878
Benaderen van een (klein) logaritme
Laten we even een Taylor expansie vergeten, die geeft voor de eerste paar termen sowieso een overschatting; ik zit met een opgave waarin de uitdrukking $$\ln 4$$ een rol speelt. En hoewel ik de opgave goed heb afgerond, blijft dit benaderen door m'n hoofd spoken. Het is een stukje nieuwsgierigheid d...
- 13 jun 2017, 18:18
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Trig. vergelijking oplossen
- Reacties: 4
- Weergaves: 5823
Re: Trig. vergelijking oplossen
Eeh ja natuurlijk. Was even snek uit de losse pols op kantoor 
- 13 jun 2017, 12:45
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Trig. vergelijking oplossen
- Reacties: 4
- Weergaves: 5823
Re: Trig. vergelijking oplossen
Ah ja natuurlijk doh! Och dankje wel, maar wat haat ik dit soort OHJA momentjes :lol: Zal het nog even uit typen, mocht iemand er tegen aan lopen. 2(\frac{\sqrt 3}{2} + 2 \sin x \cos x) = 0 \frac{\sqrt 3}{2} + 2 \sin x \cos x = 0 , dus \cos(2x) = - \frac{\sqrt 3}{2} substitueer y = 2x Als \cos(y) = ...
- 13 jun 2017, 11:36
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Trig. vergelijking oplossen
- Reacties: 4
- Weergaves: 5823
Trig. vergelijking oplossen
Vind alle oplossingen voor x, als: \frac{\sqrt3}{\sin^2 x} + 4 \cot x = 0 . Nou heb ik in eerste instantie beide zijden met \sin^2 x vermeningvuldigd, vervolgens de \cot x herschreven, om op: \sqrt 3 + 4 \sin x \cos x = 0 uit te komen. Maar hier zit ik vast, ik ken geen identiteiten of andere manier...
- 26 mar 2017, 14:42
- Forum: Analyse & calculus
- Onderwerp: Oplossing na impliciet differentieren
- Reacties: 1
- Weergaves: 3604
Oplossing na impliciet differentieren
Geef 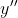 van
van 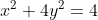 .
.
Ik heb dit uitgewerkt naar:
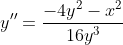
Op zich klopt dit, maar in de uitwerken staat nog een vereenvoudiging:
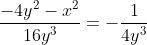
Die stap begrijp ik niet... kan iemand die nader toelichten?
Ik heb dit uitgewerkt naar:
Op zich klopt dit, maar in de uitwerken staat nog een vereenvoudiging:
Die stap begrijp ik niet... kan iemand die nader toelichten?
- 28 jan 2017, 10:48
- Forum: Analyse & calculus
- Onderwerp: Vind 2 rechte lijnen die de grafiek raken
- Reacties: 4
- Weergaves: 5946
Re: Vind 2 rechte lijnen die de grafiek raken
Oke, maar hoe kan ik daar dan een vergelijking voor vinden?
Of beter gezegd hoe kan ik dan in z'n algemeenheid alle raaklijnen door een bepaald punt vinden?
Of beter gezegd hoe kan ik dan in z'n algemeenheid alle raaklijnen door een bepaald punt vinden?
- 28 jan 2017, 09:03
- Forum: Analyse & calculus
- Onderwerp: Vind 2 rechte lijnen die de grafiek raken
- Reacties: 4
- Weergaves: 5946
Vind 2 rechte lijnen die de grafiek raken
Vind 2 rechte lijnen die 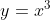 raken en door het punt
raken en door het punt ) gaan.
gaan.
Nou de eerste is natuurlijk makkelijk, differentieer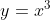 . Bepaal
. Bepaal 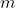 , door
, door 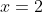 in te vullen. Gebruik point-slope, levert:
in te vullen. Gebruik point-slope, levert: 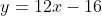 .
.
Wat is echter niet begrijp is wat er met die tweede lijn bedoeld wordt.
Nou de eerste is natuurlijk makkelijk, differentieer
Wat is echter niet begrijp is wat er met die tweede lijn bedoeld wordt.
- 21 jan 2017, 13:43
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Waarom werkt een bepaalde oplossingsrichting niet?
- Reacties: 9
- Weergaves: 10937
Re: Waarom werkt een bepaalde oplossingsrichting niet?
In je eerste methode verwaarloos je een term in beide wortels die naar oneindig gaat ... Ok, dus dat is sowieso al fout. Als ik dat tegenkom, moet ik een andere strategie zoeken? Het gaat me er vooral om waarom de andere manieren niet werken, zodat ik m'n werk beter kan maken... Het gaat me vooral ...
- 21 jan 2017, 08:57
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Waarom werkt een bepaalde oplossingsrichting niet?
- Reacties: 9
- Weergaves: 10937
Re: Waarom werkt een bepaalde oplossingsrichting niet?
Ja hoor, \lim_{x \to -\infty}(\sqrt{x^2 + 2x}-\sqrt{x^2-2x}) \lim_{x \to -\infty}\frac{x^2 + 2x - (x^2 - 2x)}{(\sqrt{x^2 + 2x} + \sqrt{x^2-2x})} \lim_{x \to -\infty}\frac{4x}{(\sqrt{x^2 + 2x} + \sqrt{x^2-2x})} \lim_{x \to -\infty}\frac{4x}{(x\sqrt{1 + \frac{2}{x}} + x\sqrt{1 - \frac{2}{x}})} Aangezi...
- 20 jan 2017, 21:18
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Waarom werkt een bepaalde oplossingsrichting niet?
- Reacties: 9
- Weergaves: 10937
Re: Waarom werkt een bepaalde oplossingsrichting niet?
@Safex met behulp van de geconjugeerde heb ik het ook uitgewerkt idd.
Maar ik behandel dus oneindig als getal. Op het moment dat ik 2 termen naar oneindig heb, zou er dus al een belletje moeten rinkelen aangezien ik daar verder niet zoveel mee kan?
@manus, het antwoord is -2
Maar ik behandel dus oneindig als getal. Op het moment dat ik 2 termen naar oneindig heb, zou er dus al een belletje moeten rinkelen aangezien ik daar verder niet zoveel mee kan?
@manus, het antwoord is -2
- 20 jan 2017, 11:53
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Waarom werkt een bepaalde oplossingsrichting niet?
- Reacties: 9
- Weergaves: 10937
Waarom werkt een bepaalde oplossingsrichting niet?
Gevraagd: \lim_{x \to -\infty}(\sqrt{x^2 + 2x} - \sqrt{x^2 - 2x}) (Adams hfst. 1.3, opg 29). Een eerste, foutieve, benadering zou kunnen zijn: Aangezien de x^2 termen leidend zijn ten opzicht van de 2x termen, blijft simpelweg \lim_{x \to -\infty}(\sqrt{x^2} - \sqrt{x^2}) over, wat 0 is. Om wat op t...
- 19 jan 2017, 11:55
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Uitwerking met absolute waarde onduidelijk
- Reacties: 3
- Weergaves: 4616
Re: Uitwerking met absolute waarde onduidelijk
x gaat naar -oneindig, dus x is negatief.
Klopt dit?
- 18 jan 2017, 18:52
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Uitwerking met absolute waarde onduidelijk
- Reacties: 3
- Weergaves: 4616
Uitwerking met absolute waarde onduidelijk
In een uitwerking van een opdracht staat de volgende stap, maar ik begrijp deze niet echt.
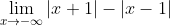
wordt omgeschreven als:
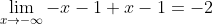
Ik begrijp de achterliggende gedacht niet echt... Kan iemand deze iets verduidelijken?
wordt omgeschreven als:
Ik begrijp de achterliggende gedacht niet echt... Kan iemand deze iets verduidelijken?
- 13 jan 2016, 16:47
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Goniometrische vergelijkingen
- Reacties: 4
- Weergaves: 4576
Re: Goniometrische vergelijkingen
ja daar heb je gelijk in hehe