Er zijn 1084 resultaten gevonden
- 25 dec 2013, 12:17
- Forum: Analyse & calculus
- Onderwerp: Oplossen limieten zonder Hopital
- Reacties: 3
- Weergaves: 5234
Re: Oplossen limieten zonder Hopital
Je hebt een limiet met een tangens erin en een uitdrukking in x. Het kan niet anders dan dat je de formule (met sinus en een uitdrukking in x) \lim_{x\to 0}\frac{\sin(x)}{x} = 1 nodig zult hebben. Echter je limiet is voor x\to 1 . Dat zal je eerst om moeten zetten naar een uitdrukking met x\to 0 . D...
- 06 nov 2013, 09:30
- Forum: Wiskundige puzzels
- Onderwerp: Wasdraad puzzel
- Reacties: 10
- Weergaves: 11868
Re: Wasdraad puzzel
deze touw hangt twee maal vier door Ik hou wel van dit soort grapjes. Het probleem is alleen dat ik bovenstaande zin niet begreep. 'Deze' touw moet natuurlijk dit touw zijn, want touw is onzijdig. Maar afgezien daarvan begrijp ik niet wat 'twee maal vier doorhangen' betekent. Hoe was het gisteren o...
- 03 nov 2013, 11:17
- Forum: Wiskundige puzzels
- Onderwerp: Zoek een wiskundige aanpak voor onderstaand probleem
- Reacties: 3
- Weergaves: 4583
Re: Zoek een wiskundige aanpak voor onderstaand probleem
Als de verdeling is 0, 33,33,34 dan is jouw aanpak problematisch. Stel je begint niet met 10,10,10,10, maar met 0,0,0,0. Je hoort b.v. dat de eerste de grootste afwijking heeft. Dan is de eerste groter dan 25 (de grootste is immers meer dan het gemiddelde). Je probeert dan 25,0,0,0. Stel nu dat verv...
- 27 sep 2013, 12:36
- Forum: Tutorials en Minicursussen
- Onderwerp: driehoeken en quaternionen
- Reacties: 0
- Weergaves: 16605
driehoeken en quaternionen
Op deze site vond ik de volgende aardige benaderingen van Quaternionen m.b.v. driehoeken. V = \{(A,B,C) | A,B,C \in \mathbb{R}^3 \wedge A \neq B \} . Een element van V noemen we een geordende driehoek. We maken nog een afbeelding die aan een geordende driehoek zijn in- en uitproduct toevoegt f : V \...
- 23 sep 2013, 17:56
- Forum: Voortgezet onderwijs bovenbouw / 2de en 3de graad ASO
- Onderwerp: Hoe los ik dit op: 3^x * 4^x+2 = 8
- Reacties: 15
- Weergaves: 13351
Re: Hoe los ik dit op: 3^x * 4^x+2 = 8
RaRa?SafeX schreef:Het is een RR:
- 20 sep 2013, 13:58
- Forum: Wiskunde studeren
- Onderwerp: wat is een AXIOMA?
- Reacties: 1
- Weergaves: 8096
Re: wat is een AXIOMA?
Stel je wilt een marsmannetje uitleggen wat rekenen is. Dan wil je eerst uitleggen wat getallen zijn. Je begint natuurlijk met de makkelijkste getallen, 1,2,3,... Maar hoe doe je dat. We zoeken naar regels die de natuurlijke getallen beschrijven. Bijvoorbeeld zo: Regel 1: Er is een kleinste getal, w...
- 18 sep 2013, 10:35
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
Bij 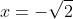 zijn er 9 ophopingspunten waar de rij naar "convergeert".
zijn er 9 ophopingspunten waar de rij naar "convergeert".
De rij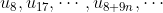
convergeert niet naar 1.
Deze rij convergeert wel heel snel, elke term geeft 40 extra decimalen.
u(8)-u(0) ~ 10^-44
u(17)-u(8) ~ 10^-84
u(26)-u(17) ~ 10^-124
u(35)-u(26) ~ 10^-164
De rij
convergeert niet naar 1.
Deze rij convergeert wel heel snel, elke term geeft 40 extra decimalen.
u(8)-u(0) ~ 10^-44
u(17)-u(8) ~ 10^-84
u(26)-u(17) ~ 10^-124
u(35)-u(26) ~ 10^-164
- 17 sep 2013, 13:43
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
Je 26-ste regel lijkt 1 te zijn.
Dat is niet zo, het is
1,000000000000000000000000000000000000000000004994175...+ 1.513...E-45*I
Curieus.
Dat is niet zo, het is
1,000000000000000000000000000000000000000000004994175...+ 1.513...E-45*I
Curieus.
- 17 sep 2013, 13:20
- Forum: Wiskunde studeren
- Onderwerp: Binomium van newton (is dit correct?)
- Reacties: 3
- Weergaves: 9392
Re: Binomium van newton (is dit correct?)
wortel2 vervangen door \sqrt{2}
Je zou toch tussen die twee regels een =teken verwachten.sacha schreef:
- 16 sep 2013, 16:47
- Forum: De Wiskundelounge
- Onderwerp: lastig
- Reacties: 2
- Weergaves: 15854
Re: lastig
Ik kan wel wat.
- 16 sep 2013, 08:04
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
u_{0} = \sqrt{2} u_{n} = \sqrt{2}^{u_{n-1}} voor n>0. Met volledige inductie is hieruit aan te tonen dat u_{n}\le 2 voor alle n. Het klopt voor n=0. Stel u_{m}\le 2 , dan is u_{m+1} = \sqrt{2}^{u_{m}} \le\mbox{ (} inductiehypothese en x\to\sqrt{2}^x is stijgend \mbox{) }\sqrt{2}^2 = 2 .
- 16 sep 2013, 07:35
- Forum: Analyse & calculus
- Onderwerp: differentiaalvgl oplossen met machtreeksmethode
- Reacties: 10
- Weergaves: 13920
Re: differentiaalvgl oplossen met machtreeksmethode
In het boek staat een héél ander probleem. Hier is gegeven dat y(0)=0.
In dat geval is het mogelijk; in het algemene geval volstrekt onmogelijk.
In dat geval is het mogelijk; in het algemene geval volstrekt onmogelijk.
- 15 sep 2013, 15:11
- Forum: Analyse & calculus
- Onderwerp: differentiaalvgl oplossen met machtreeksmethode
- Reacties: 10
- Weergaves: 13920
Re: differentiaalvgl oplossen met machtreeksmethode
Dat gaat niet.
Neem de oplossing) .
.
De functie bestaat niet eens in 0.
Neem de oplossing
De functie bestaat niet eens in 0.
- 15 sep 2013, 12:41
- Forum: Analyse & calculus
- Onderwerp: differentiaalvgl oplossen met machtreeksmethode
- Reacties: 10
- Weergaves: 13920
Re: differentiaalvgl oplossen met machtreeksmethode
Dit probleem is niet geschikt om met machtreeksen op te lossen.
- 14 sep 2013, 07:20
- Forum: Analyse & calculus
- Onderwerp: ff opfrissen
- Reacties: 4
- Weergaves: 9654
Re: ff opfrissen
Substitueer
dan
enz.