Er zijn 1084 resultaten gevonden
- 13 sep 2013, 12:14
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdots}} = 4 komt niet uit de lucht vallen. Het is jouw truc die uit de lucht komt vallen. \sqrt{2} is geen oplossing als bij substitutie er niet 2 maar 4 uit komt. Om \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdots}} te berekenen stel ik het gelijk aan y. \sqrt{2}^{\sqrt{2}^{\sq...
- 13 sep 2013, 08:49
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
Los op
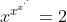 .
.
Wat denk je van de volgende redenering:
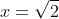 kan geen oplossing zijn, want dan komt er 4 uit
kan geen oplossing zijn, want dan komt er 4 uit
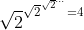
Ga maar na met je truc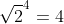 .
.
Wat denk je van de volgende redenering:
Ga maar na met je truc
- 13 sep 2013, 07:43
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
Welk argument heb je daar voor? Stijgend en begrensd?David schreef: Wat 2 nadert als n toeneemt.
- 12 sep 2013, 21:00
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
Misschien zijn er wel géén oplossingen.
Geloof je dat mijn oplossing een echte oplossing is?
Ik ben daar niet zo zeker van.
Zonder convergentiebewijs overtuigt me geen enkele truc.
Geloof je dat mijn oplossing een echte oplossing is?
Ik ben daar niet zo zeker van.
Zonder convergentiebewijs overtuigt me geen enkele truc.
- 12 sep 2013, 18:21
- Forum: Wiskundige puzzels
- Onderwerp: machtsverheffingen van x
- Reacties: 24
- Weergaves: 27189
Re: machtsverheffingen van x
Volgens mijn truc zou de uitkomst moeten zijn
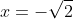
Klopt dat?
Vind je mijn truc overtuigend?
Klopt dat?
Vind je mijn truc overtuigend?
- 11 sep 2013, 08:32
- Forum: Voortgezet onderwijs / 1ste graad ASO-TSO-BSO
- Onderwerp: Merkwaardige producten
- Reacties: 5
- Weergaves: 6739
Re: Merkwaardige producten
Als je om je tekst
(p-2q)(p+2q)(p^2-q^2) [tex] en [/tex] schrijft,
dus zo
[tex] (p-2q)(p+2q)(p^2-q^2) [/tex]
dan krijg je (zie hoe mooi en duidelijk!)
(p+2q)(p^2-q^2))
(p-2q)(p+2q)(p^2-q^2) [tex] en [/tex] schrijft,
dus zo
[tex] (p-2q)(p+2q)(p^2-q^2) [/tex]
dan krijg je (zie hoe mooi en duidelijk!)
- 10 sep 2013, 16:05
- Forum: Hoger onderwijs - overig
- Onderwerp: Wortels en breuken
- Reacties: 10
- Weergaves: 10436
Re: Wortels en breuken
Aan te tonen is dat ^{3} = \frac{1}{4}\sqrt2)
Concentreer je eerst alleen op het vereenvoudigen van
 .
.
 (zie de rekenregels bij mkamminga).
(zie de rekenregels bij mkamminga).
Concentreer je eerst alleen op het vereenvoudigen van
- 09 sep 2013, 17:11
- Forum: Analyse & calculus
- Onderwerp: Aantonen nulverzameling
- Reacties: 10
- Weergaves: 11787
Re: Aantonen nulverzameling
Een verzameling U is nul als er een oneindige rij verzamelingen bestaat
) die in oppervlakte/lengte/inhoud naar 0 gaan. U hoeft niet leeg te zijn.
die in oppervlakte/lengte/inhoud naar 0 gaan. U hoeft niet leeg te zijn.
- 09 sep 2013, 08:01
- Forum: Hoger onderwijs - overig
- Onderwerp: Volledige inductie
- Reacties: 4
- Weergaves: 4322
Re: Volledige inductie
Systematisch:
Je weet
Je wilt aantonen
Nu is
 (volledige inductie)
(volledige inductie) 
Rest nog om aan te tonen dat

Je weet
Je wilt aantonen
Nu is
Rest nog om aan te tonen dat
- 07 sep 2013, 10:57
- Forum: Wiskundige puzzels
- Onderwerp: Plezante vergelijking
- Reacties: 20
- Weergaves: 18452
Re: Plezante vergelijking
Dat levert



- 06 sep 2013, 11:03
- Forum: Wiskundige puzzels
- Onderwerp: Plezante vergelijking
- Reacties: 20
- Weergaves: 18452
Re: Plezante vergelijking
De vraag is dus, hoe je eenvoudig probleem door slimme trucs in een moeilijk probleem kunt omtoveren.
- 06 sep 2013, 10:54
- Forum: Wiskundige puzzels
- Onderwerp: kan dit met lineair programmeren opgelost worden?
- Reacties: 7
- Weergaves: 7049
Re: kan dit met lineair programmeren opgelost worden?
Nee, maar je kunt het op dit forum zetten (met namen als A,B,C,... of 1,2,3,...) en wie weet is iemand op dit forum bereid een oplossing te geven.
- 06 sep 2013, 07:40
- Forum: Wiskundige puzzels
- Onderwerp: kan dit met lineair programmeren opgelost worden?
- Reacties: 7
- Weergaves: 7049
Re: kan dit met lineair programmeren opgelost worden?
Dit is geen lineair programmeringsprobleem, maar een grafentheoretisch probleem.
- 06 sep 2013, 07:36
- Forum: Wiskundige puzzels
- Onderwerp: Plezante vergelijking
- Reacties: 20
- Weergaves: 18452
Re: Plezante vergelijking
Nee, rechttoe rechtaan oplossen geeft een lineaire vergelijking.
- 05 sep 2013, 17:29
- Forum: Analyse & calculus
- Onderwerp: Riemann-integreerbaar
- Reacties: 5
- Weergaves: 7248
Re: Riemann-integreerbaar
Kies  zeer klein.
zeer klein.
Kies partitie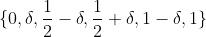
Geeft nu een afschatting voor de bovensom.
De ondersom = 0. Waarom?
Kies partitie
Geeft nu een afschatting voor de bovensom.
De ondersom = 0. Waarom?