Parabool en elips
Parabool en elips
Hoi,
Wie kan mij helpen ?
Ik moet twee vrij grote parabolen tekenen op roestvrijstaal.
Als ik nu een elips teken met behulp van twee vaste punten, een touwtje en een viltstift en ik zaag vervolgens de plaat precies in twee stukken, heb ik dan op elke plaat een parabool ?
Dus eigenlijk is de vraag of een halve elips hetzelfde is als een parabool.
Groetjes en bedankt !
Pieter
Wie kan mij helpen ?
Ik moet twee vrij grote parabolen tekenen op roestvrijstaal.
Als ik nu een elips teken met behulp van twee vaste punten, een touwtje en een viltstift en ik zaag vervolgens de plaat precies in twee stukken, heb ik dan op elke plaat een parabool ?
Dus eigenlijk is de vraag of een halve elips hetzelfde is als een parabool.
Groetjes en bedankt !
Pieter
Re: Parabool en elips
Een parabool is NIET hetzelfde als een halve ellips.
Om dit te bewijzen kijk je bijvoorbeeld naar de raaklijnen aan de ellips op de snijpunten met de assen, en vergelijk dit met die van een parabool.
Om dit te bewijzen kijk je bijvoorbeeld naar de raaklijnen aan de ellips op de snijpunten met de assen, en vergelijk dit met die van een parabool.
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Parabool en elips
Zie voor meer info http://nl.wikipedia.org/wiki/Kegelsnede
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Parabool en elips
Hallo,
Bedankt voor de reacties en sorry voor de spelfout. Het moet natuurlijk "ellips" zijn.
Is er een trucje, zoals een passer bij het tekenen van een cirkel of een touwtje rond twee vaste punten voor het tekenen van een ellips, om een parabool een beetje netjes te tekenen ?
Of is het gewoon een kwestie van een heleboel punten bepalen ?
Groetjes en bedankt maar weer.
Pieter
Bedankt voor de reacties en sorry voor de spelfout. Het moet natuurlijk "ellips" zijn.
Is er een trucje, zoals een passer bij het tekenen van een cirkel of een touwtje rond twee vaste punten voor het tekenen van een ellips, om een parabool een beetje netjes te tekenen ?
Of is het gewoon een kwestie van een heleboel punten bepalen ?
Groetjes en bedankt maar weer.
Pieter
Re: Parabool en elips
Ik word er gek van.
Hoe stel je nou ook alweer een vergelijking van parabool op ?
Top = 36,0
punt : (10,102)
Punt : (62,102)
Ik krijg steeds een negatieve a en dus bergparabool, maar het moet een dal zijn.
Wie, o wie frist mijn geheugen op ?
Bedankt !
Hoe stel je nou ook alweer een vergelijking van parabool op ?
Top = 36,0
punt : (10,102)
Punt : (62,102)
Ik krijg steeds een negatieve a en dus bergparabool, maar het moet een dal zijn.
Wie, o wie frist mijn geheugen op ?
Bedankt !
Re: Parabool en elips
Gebruik de algemene formule van een parabool:
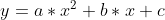
Vul hier de punten in die je al hebt: top=(36,0) en verder de punten (10,102) en (62,102).
Er ontstaat dan een stelsel van 3 vergelijkingen met 3 onbekenden:
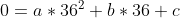
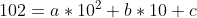
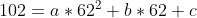
Los dit stelsel op en je vindt bij benadering:
a=0.150887574
b=-10.86390533
c=195.5502958
Dus je parabool heeft de vergelijking:
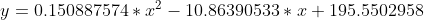
en hiermee kan je al je overige punten vinden.
Ter controle:
Vul hier de punten in die je al hebt: top=(36,0) en verder de punten (10,102) en (62,102).
Er ontstaat dan een stelsel van 3 vergelijkingen met 3 onbekenden:
Los dit stelsel op en je vindt bij benadering:
a=0.150887574
b=-10.86390533
c=195.5502958
Dus je parabool heeft de vergelijking:
en hiermee kan je al je overige punten vinden.
Ter controle:
Code: Selecteer alles
X Y
0 195.55
1 184.84
2 174.43
3 164.32
4 154.51
5 145.00
6 135.80
7 126.90
8 118.30
9 110.00
10 102.00
11 94.30
12 86.91
13 79.82
14 73.03
15 66.54
16 60.36
17 54.47
18 48.89
19 43.61
20 38.63
21 33.95
22 29.57
23 25.50
24 21.73
25 18.26
26 15.09
27 12.22
28 9.66
29 7.39
30 5.43
31 3.77
32 2.41
33 1.36
34 0.60
35 0.15
36 0.00
37 0.15
38 0.60
39 1.36
40 2.41
41 3.77
42 5.43
43 7.39
44 9.66
45 12.22
46 15.09
47 18.26
48 21.73
49 25.50
50 29.57
51 33.95
52 38.63
53 43.61
54 48.89
55 54.47
56 60.36
57 66.54
58 73.03
59 79.82
60 86.91
61 94.30
62 102.00
63 110.00
64 118.30
65 126.90
66 135.80
67 145.00
68 154.51
69 164.32
70 174.43
71 184.84
72 195.55
Re: Parabool en elips
Super, hartstikke bedankt !
Nu kan ik m'n "design" tafel tenminste fatsoenlijk afmaken.
Groetjes,
Pieter.
Nu kan ik m'n "design" tafel tenminste fatsoenlijk afmaken.
Groetjes,
Pieter.
Re: Parabool en elips
Mag ik nog wat vragen ?
De perfecte cirkel teken je met een middelpunt, een touwtje en een balpen.
De perfecte ellips met twee punten, een touwtje en een pen.
Hoe teken je op soortgelijke manier de perfecte parabool ?
Ik begrijp dat dat in ieder geval kan, door heel veel punten uit te zetten, maar is er ook zoiets mogelijk als met cirkel en ellips ?
Alvast opnieuw heel erg bedankt.
Groetjes,
Pieter.
De perfecte cirkel teken je met een middelpunt, een touwtje en een balpen.
De perfecte ellips met twee punten, een touwtje en een pen.
Hoe teken je op soortgelijke manier de perfecte parabool ?
Ik begrijp dat dat in ieder geval kan, door heel veel punten uit te zetten, maar is er ook zoiets mogelijk als met cirkel en ellips ?
Alvast opnieuw heel erg bedankt.
Groetjes,
Pieter.
Re: Parabool en ellips
Ik ken geen eenvoudige en efficiente methode (vergelijkbaar met cirkel en ellips) om een parabool te tekenen.
Er zijn wel een aantal constructies, zie bijvoorbeeld http://www.pandd.demon.nl/parab/parab.htm, maar volgens mij geven deze niet echt voordeel boven uitrekenen en tekenen van punten.
Je kan natuurlijk wel een mal maken, bijvoorbeeld van een stuk karton of triplex, dan heb je maar een halve parabool nodig: deze kan je vervolgens omklappen om de symmetrie-as om de andere helft op je metaalplaat te tekenen.
Wat ook nog zou kunnen doen is de parabool tekenen mbv je computer en
- deze laten printen op posterformaat, maar dit lijkt me een kostbare oplossing
- op je metalen platen projecteren met een beamer en dan overtrekken, maar ik weet niet of dit echt handig/nauwkeurig gaat...
Wellicht hebben andere forum-leden meer/betere suggesties...
Er zijn wel een aantal constructies, zie bijvoorbeeld http://www.pandd.demon.nl/parab/parab.htm, maar volgens mij geven deze niet echt voordeel boven uitrekenen en tekenen van punten.
Je kan natuurlijk wel een mal maken, bijvoorbeeld van een stuk karton of triplex, dan heb je maar een halve parabool nodig: deze kan je vervolgens omklappen om de symmetrie-as om de andere helft op je metaalplaat te tekenen.
Wat ook nog zou kunnen doen is de parabool tekenen mbv je computer en
- deze laten printen op posterformaat, maar dit lijkt me een kostbare oplossing
- op je metalen platen projecteren met een beamer en dan overtrekken, maar ik weet niet of dit echt handig/nauwkeurig gaat...
Wellicht hebben andere forum-leden meer/betere suggesties...
Re: Parabool en elips
Ik heb misschien wel een idee om een parabool te construeren. Om dit in de praktijk te doen, moet men wel "handig" zijn; het is wat omslachtig. Ik hoop dat het nog op tijd is.
Wat je nodig hebt (ik weet niet veel over goede materiaalkeuze, ik ga uit van hout)\
-4 houten staven/planken, zolang het maar recht is. 1 voor lijn M, een voor het lijnstuk, een voor de loodlijn en een voor de middelloodlijn (zie toelichting, afmeting afhankelijk van formaat parabool) Op de planken moet een ringetje kunnen schuiven.
-4 ringen o.i.d, twee die mee kan draaien in hout, een in het metaal.
-touw (schuift het lijnstuk overheen, zie toelichtende tekst
-bijv. een potlood om de parabool mee te construeren.
De constructie van de parabool:
Een parabool is een figuur waarop de punten even ver liggen van een punt P en een lijn M. Als je een punt van de parabool wil construeren, kies je een punt op de lijn en tekent daar een loodlijn in.
Verbind het punt op de lijn met het losse punt. Die verbinding vormt een lijnstuk A. Teken een middelloodlijn van A. De middelloodlijn snijdt de loodlijn op M in S. Alle punten S vormen een parabool.
De praktijk:
De lijn M is een stuk hout. In dat stuk hout komt een ring die te verschuiven is op het hout. Die ring kan ook nog draaien. Uit dat punt loopt tevens een loodlijn, die door verschuiven meebeweegt. Door het ringetje dat kan draaien komt een staafje, die vrij door de ring kan bewegen. In het losse punt P komt ook een ring met dezelfde staaf erdoorheen. die beweegt dus mee. Het punt voor de middelloodlijn verschuift over een lijn evenwijdig aan lijn M, precies tussen het punt P en lijn M. Op het lijnstuk komt ook een middelloodlijn. Op de middelloodlijn komt een ringetje waar bijv. een potlood doorheengaat. Die schuift mee op de middelloodlijn. Dat potlood wordt ook zo verbonden met de loodlijn van M. Het schuiven van het potlood zou bijv. kunnen op iets als een gordijnrails. Als het goed gemaakt wordt, zou je zo een parabool kunnen maken. Is het zo duidelijk? Het
Wat je nodig hebt (ik weet niet veel over goede materiaalkeuze, ik ga uit van hout)\
-4 houten staven/planken, zolang het maar recht is. 1 voor lijn M, een voor het lijnstuk, een voor de loodlijn en een voor de middelloodlijn (zie toelichting, afmeting afhankelijk van formaat parabool) Op de planken moet een ringetje kunnen schuiven.
-4 ringen o.i.d, twee die mee kan draaien in hout, een in het metaal.
-touw (schuift het lijnstuk overheen, zie toelichtende tekst
-bijv. een potlood om de parabool mee te construeren.
De constructie van de parabool:
Een parabool is een figuur waarop de punten even ver liggen van een punt P en een lijn M. Als je een punt van de parabool wil construeren, kies je een punt op de lijn en tekent daar een loodlijn in.
Verbind het punt op de lijn met het losse punt. Die verbinding vormt een lijnstuk A. Teken een middelloodlijn van A. De middelloodlijn snijdt de loodlijn op M in S. Alle punten S vormen een parabool.
De praktijk:
De lijn M is een stuk hout. In dat stuk hout komt een ring die te verschuiven is op het hout. Die ring kan ook nog draaien. Uit dat punt loopt tevens een loodlijn, die door verschuiven meebeweegt. Door het ringetje dat kan draaien komt een staafje, die vrij door de ring kan bewegen. In het losse punt P komt ook een ring met dezelfde staaf erdoorheen. die beweegt dus mee. Het punt voor de middelloodlijn verschuift over een lijn evenwijdig aan lijn M, precies tussen het punt P en lijn M. Op het lijnstuk komt ook een middelloodlijn. Op de middelloodlijn komt een ringetje waar bijv. een potlood doorheengaat. Die schuift mee op de middelloodlijn. Dat potlood wordt ook zo verbonden met de loodlijn van M. Het schuiven van het potlood zou bijv. kunnen op iets als een gordijnrails. Als het goed gemaakt wordt, zou je zo een parabool kunnen maken. Is het zo duidelijk? Het
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: Parabool en elips
Voor de parabool kom ik exact uit op
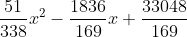
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
(Raffiek Torreman)
Re: Parabool en elips
Goede dag,arie schreef:Gebruik de algemene formule van een parabool:
Vul hier de punten in die je al hebt: top=(36,0) en verder de punten (10,102) en (62,102).
Er ontstaat dan een stelsel van 3 vergelijkingen met 3 onbekenden:
Los dit stelsel op en je vindt bij benadering:
a=0.150887574
b=-10.86390533
c=195.5502958
Dus je parabool heeft de vergelijking:
Ik heb een vraag die op dit antwoord lijkt.
In Basisboek wiskunde blz 126 moet je een vergelijking maken waarbij je slechts 2 punten krijgt (top en een punt) Zou iemand mij kunnen vertellen hoe ik dat moet oplossen. Alvast heel erg bedankt.
(som) 16.15 A Top (x,y) (1,2) Punt (2,3)
goede antwoord:
16.15 C Top (2,-1) Punt (1,1)
........
Antwoord:
16.14 D Top (3,0) punt (-1,-2)
........
Antwoord:
Arno heel erg bedankt voor je reactie, Ik heb hem bijgewerkt.
Laatst gewijzigd door dave0065 op 12 jul 2010, 14:59, 3 keer totaal gewijzigd.
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Parabool en elips
Als (p,q) de top van de parabool is, dan is de vergelijking van de parabool te schrijven als y = a(x-p)²+q. Indien (r,s) een bekend punt is kun je door dit in de topvergelijking in te vullen de waarde voor a vinden.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Parabool en elips
Een parabool, cirkel, ellips en hyperbool zijn allen kegeldoorsnedes en hebben zeker wat met elkaar te maken.
Parabolen, cirkels en ellipsen kun je met een touwtje construeren (tekenen zo je wilt).
Hoe het met de hyperbool moet weet ik nog niet.
De truck is dat je vanuit het brandpunt een touwtje neemt en dat met een tekenhaak parallel verschuift,
Zodat je voldoet aan de eigenschap : de afstand van brandpunt, een punt op de parabool en tot een lijn loodrecht op de symmetrie-as steeds gelijk is.
1. Sla een spijker in het brandpunt en maak daar het touwtje vast.
2. Leg de tekenhaak tegen de tafelrand en tegen de spijker.
3. Neem voor de lengte van het touwtje de dubbele brandpuntsafstand en maak het andere uiteinde vast onder aan de tekenhaak.
4. Steek je pen met rechte schacht onder het touwtje en trekt het strak naar de top.
5. Door nu de tekenhaak te verschuiven , volgt de punt van de pen de parabool ( een helft ).
6. Leg de tekenhaak aan de andere kant van de spijker en je krijgt de andere kant van de parabool.
Ik heb zo zelf parabolen getekend van een meter in x-as.
Parabolen, cirkels en ellipsen kun je met een touwtje construeren (tekenen zo je wilt).
Hoe het met de hyperbool moet weet ik nog niet.
De truck is dat je vanuit het brandpunt een touwtje neemt en dat met een tekenhaak parallel verschuift,
Zodat je voldoet aan de eigenschap : de afstand van brandpunt, een punt op de parabool en tot een lijn loodrecht op de symmetrie-as steeds gelijk is.
1. Sla een spijker in het brandpunt en maak daar het touwtje vast.
2. Leg de tekenhaak tegen de tafelrand en tegen de spijker.
3. Neem voor de lengte van het touwtje de dubbele brandpuntsafstand en maak het andere uiteinde vast onder aan de tekenhaak.
4. Steek je pen met rechte schacht onder het touwtje en trekt het strak naar de top.
5. Door nu de tekenhaak te verschuiven , volgt de punt van de pen de parabool ( een helft ).
6. Leg de tekenhaak aan de andere kant van de spijker en je krijgt de andere kant van de parabool.
Ik heb zo zelf parabolen getekend van een meter in x-as.

