Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
Bagration
- Nieuw lid

- Berichten: 11
- Lid geworden op: 28 jul 2018, 19:17
Bericht
door Bagration » 06 aug 2019, 16:51
Hallo,
Bij onderstaand vraagstuk moet men een bepaalde afstand berekenen om de snelste weg te bekomen.
Wel heb ik gevonden dat x0=
)
en dat vervolgens
)
.
Kan iemand mij verder helpen hoe ik dit verder oplos?
https://imgur.com/CQbs3gh
-
arie
- Moderator

- Berichten: 3916
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 06 aug 2019, 18:50
De totale lengte van de spoorlijn op het plaatje is
\(L_{spoor} = \sqrt{130^2 - 50^2} = 120\) km
Gebruik verder:
\(afstand = snelheid \cdot tijd\)
ofwel:
\(tijd = \frac{afstand}{snelheid} \)
De afstand die de trein moet afleggen is:
(de totale lengte spoorlijn) - X1 = 120 - X1
De tijd die de trein daarover doet is
\(t_{trein}=\frac{120-X1}{100}\)
Je had zelf al gevonden dat de bus moet afleggen:
\(X0 = \sqrt{2500 + X1^2}\)
De tijd die de bus daarover doet is
\(t_{bus}=\frac{\sqrt{2500 + X1^2}}{60}\)
De vraag is nu: voor welke X1 is de totale reistijd minimaal, ofwel: voor welke X1 is
\(t_{totaal} = t_{trein}+t_{bus}\)
minimaal?
Kom je hiermee verder?
-
Bagration
- Nieuw lid

- Berichten: 11
- Lid geworden op: 28 jul 2018, 19:17
Bericht
door Bagration » 06 aug 2019, 20:06
Bedankt voor de hulp. Dit heeft me heel wat geholpen.
Wat ik niet goed snap is dat men een minimum kan zoeken voor de totale tijd wanneer x1 onbekend is.
Ttrein: (120-
x1)/100
en
Tbus: (120-
x1)/60
Alvast bedankt

-
arie
- Moderator

- Berichten: 3916
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 06 aug 2019, 20:33
De enige variabele die we kunnen beinvloeden is X1 = de plaats van het station.
De tijd die de trein er over doet \(t_{trein}\) en de tijd die de bus er over doet \(t_{bus}\) hebben we hierboven beide uitgedrukt afhankelijk van X1.
De totale reistijd is de som van beide, dus ook de totale reistijd is ook afhankelijk van X1.
We hebben het dus over "de totale reistijd" als functie van X1:
\(t_{totaal} = f(X1) = t_{trein} + t_{bus}\)
ofwel:
\(t_{totaal} = f(X1) = \frac{120-X1}{100} + \frac{\sqrt{2500 + X1^2}}{60}\)
Je kan dit ook nog anders schrijven door X1 = x te maken:
\(t_{totaal} = f(x) = \frac{120-x}{100} + \frac{\sqrt{2500 + x^2}}{60}\)
Kan je nu de x vinden waarvoor \(f(x) = t_{totaal}\) minimaal is?
-
Bagration
- Nieuw lid

- Berichten: 11
- Lid geworden op: 28 jul 2018, 19:17
Bericht
door Bagration » 06 aug 2019, 21:50
Dag arie,
Na even nadenken ben ik tot een oplossing gekomen van 82,5 km (de afstand waarop het station gebouwd moet worden).
Dit door de differentiaal van volgende functie te nemen:
\(
\frac{120-x}{100} +\frac{sqrt (2500+x^2)}{60}
\)
Hierbij bekom ik volgende afgeleide:
\(
f ' (x)=\frac{-1}{100} +\frac{x}{60 sqrt(2500+x^2)}
\)
Hierbij heb ik steeds x ingevuld met een getal tot ik een minimum voor de functie bekom.
Dit is zeer veel werk om x steeds in te vullen. Is er een andere manier om x te vinden?


-
arie
- Moderator

- Berichten: 3916
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 06 aug 2019, 22:17
In een minimum (net als bij een maximum) is de afgeleide nul.
De afgeleide had je al gevonden:
\( f ' (x)=\frac{-1}{100} +\frac{x}{60 \sqrt{2500+x^2}}\)
Als je deze gelijk aan nul stelt, dan krijgen we:
\(\frac{-1}{100} +\frac{x}{60 \sqrt{2500+x^2}} = 0\)
ofwel
\(\frac{x}{60 \sqrt{2500+x^2}} = \frac{1}{100}\)
ofwel (kruislings vermenigvuldigen):
\(100x = 60 \sqrt{2500+x^2}\)
Kan je hieruit x oplossen?
-
Bagration
- Nieuw lid

- Berichten: 11
- Lid geworden op: 28 jul 2018, 19:17
Bericht
door Bagration » 07 aug 2019, 10:40
Dag arie,
Bedankt voor het snelle antwoord. Wanneer de afgeleide 0 is heeft men een minimum/maximum van de functie. Dit snap ik.
Omdat dit geen meergraadsvergelijking is, vind ik het iets moeilijker om x er uit te halen en ben ik niet echt mee met het verhaal

-
arie
- Moderator

- Berichten: 3916
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 07 aug 2019, 11:14
We hadden:
\(100x = 60 \sqrt{2500+x^2}\)
ofwel (deel links en rechts door 20 om wat kleinere getallen te krijgen):
\(5x = 3 \sqrt{2500+x^2}\)
Om het wortelteken weg te werken kwadrateren we links en rechts:
\(\left(5x \right)^2 = \left( 3 \sqrt{2500+x^2} \right)^2\)
Deze vergelijking werken we uit met de formule \((a\cdot b)^n = a^n \cdot b^n\)
Wat levert dit op voor onze vergelijking?
-
Bagration
- Nieuw lid

- Berichten: 11
- Lid geworden op: 28 jul 2018, 19:17
Bericht
door Bagration » 07 aug 2019, 11:53
Ik ben er van overtuigd dat het een eenvoudige uitwerking is maar zit wat vast

(mijn excuses als ik niet direct mee ben). De bovenstaande formule van jouw heb ik verder uitgewerkt tot:
^2=(3\sqrt{2500+x^2})^2)
)
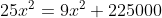
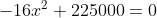
Wanneer ik hier vervolgens x uit haal, kom ik op een getal van 118,6 voor x en geen 82,5. Kan het zijn dat ik hier iets fout doe?
Alvast bedankt!!
-
arie
- Moderator

- Berichten: 3916
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 07 aug 2019, 12:12
Typfoutje: je hebt een nul te veel achter die 2500.
Zonder die extra nul krijg je:
^2=(3\sqrt{2500+x^2})^2)
)
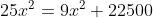
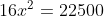 \(x^2 = \frac{22500}{16}\)
\(x^2 = \frac{22500}{16}\)
en omdat x positief moet zijn (anders zou het station verder naar links liggen dan het spoor lang is):
\(x = \sqrt{\frac{22500}{16}} = \frac{150}{4} = 37.5\)
Maar dit is de afstand x = X1 in je plaatje.
Wat is dus de afstand van de stad tot het station?
-
Bagration
- Nieuw lid

- Berichten: 11
- Lid geworden op: 28 jul 2018, 19:17
Bericht
door Bagration » 07 aug 2019, 12:25
Had dit over het hoofd gezien. Stomme fout maar nu snap ik hem!!
De afstand is dus inderdaad 82,5 km (120-x1= 120-37,5).
Bedankt voor de grondige uitleg!!

