Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
Jessie
- Nieuw lid

- Berichten: 7
- Lid geworden op: 25 sep 2013, 19:09
Bericht
door Jessie » 23 jul 2014, 13:33

beste,
Bij het oplossen van de volgende differentiaalverelijking loop ik vast. De opdracht is dat ik naga of de functie een oplossing is van de DV. Als eerste heb ik daarom de DV gedeeld door dx. Daarna had ik de functie onder logaritme geplaatst, zodat de e wegviel, echter werd mijn oplossing zo groot dat ik door de bomen het bos niet meer zag en volgens mij klopte het ook niet meer. Is er misschien iemand die me met deze opgave op weg zou kunnen helpen?
Alvast hartelijk dank
-
nielzs
- Vast lid

- Berichten: 27
- Lid geworden op: 09 jul 2014, 11:18
Bericht
door nielzs » 23 jul 2014, 18:27
De DV wordt weergegeven door een vergelijking van de vorm:
M(x,y) dx + N(x,y)dy = 0.
Een vergelijking in dergelijke vorm is ofwel een exacte DV ofwel een bijna exacte DV. Ga aan de hand van het criterium van Euler eens na of de DV exact is. Als de DVexact is, dan kun je deze oplossen, en vervolgens zal je wel merken of de voorgestelde oplossing daadwerkelijk ook een oplossing is.
Indien de DV niet exact is kun je nagaan of ze bijna exact is. Dit doe je door het zoeken van een integratiefactor µ(x) of µ(y). Hiermee kan de bijna exacte DV in een exacte DV worden omgezet. Vervolgens kun je dezelfde werkwijze hanteren als hierboven vermeld.
-
Kinu
- Moderator

- Berichten: 1144
- Lid geworden op: 22 okt 2010, 15:38
Bericht
door Kinu » 27 jul 2014, 10:46
Jessie schreef:
beste,
Bij het oplossen van de volgende differentiaalverelijking loop ik vast. De opdracht is dat ik naga of de functie een oplossing is van de DV. Als eerste heb ik daarom de DV gedeeld door dx. Daarna had ik de functie onder logaritme geplaatst, zodat de e wegviel, echter werd mijn oplossing zo groot dat ik door de bomen het bos niet meer zag en volgens mij klopte het ook niet meer. Is er misschien iemand die me met deze opgave op weg zou kunnen helpen?
Alvast hartelijk dank
Ik kan je uitwerking niet goed lezen. Kan je deze groter uploaden of in tex typen?
Het delen door
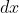
lijkt me alvast een goede stap om mee te starten.
nielzs schreef:De DV wordt weergegeven door een vergelijking van de vorm:
M(x,y) dx + N(x,y)dy = 0.
Een vergelijking in dergelijke vorm is ofwel een exacte DV ofwel een bijna exacte DV. Ga aan de hand van het criterium van Euler eens na of de DV exact is. Als de DVexact is, dan kun je deze oplossen, en vervolgens zal je wel merken of de voorgestelde oplossing daadwerkelijk ook een oplossing is.
Indien de DV niet exact is kun je nagaan of ze bijna exact is. Dit doe je door het zoeken van een integratiefactor µ(x) of µ(y). Hiermee kan de bijna exacte DV in een exacte DV worden omgezet. Vervolgens kun je dezelfde werkwijze hanteren als hierboven vermeld.
Wat je doet zal werken, maar het is denk ik niet de bedoeling om de DV te gaan oplossen. Om na te gaan of een functie een oplossing is van een DV is het gemakkelijker om de functie gewoon in te vullen en te kijken of aan de DV voldaan is ipv de DV op te lossen.
-
Jessie
- Nieuw lid

- Berichten: 7
- Lid geworden op: 25 sep 2013, 19:09
Bericht
door Jessie » 28 jul 2014, 12:22
De opgave is;
Beschouw de DV (x^2 + y^2)dx + (x^2 - xy)dy = 0
We moeten nagaan of de impliciete functie bepaald door a(x +y)^2 = xe^(y/x) een oplossing is van de DV
Daarom heb ik als eerste de DV gedeeld door dx, zodat we krijgen:
(x^2 + y^2) + (x^2 - xy)y' = 0
echter weet ik nu niet meer hoe ik verder moet. Het is inderdaad niet de bedoeling dat we nagaan of hij exact is of niet. In ieder geval al bedankt voor jullie hulp!
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 28 jul 2014, 13:15
Probeer aan te tonen dat de afgeleide van de impliciete functie voldoet aan de DV ...



