Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
Ilona
- Gevorderde

- Berichten: 100
- Lid geworden op: 13 sep 2013, 11:33
Bericht
door Ilona » 04 okt 2014, 13:56
Hoi!
Alweer een vraagje van mijn kant. Ja, ik ben druk bezig met mijn herkansingsvak en ik probeer het bewijs weer in elkaar te krijgen.
De vraag: Laat A een verzameling zijn en laat
\rightarrow P(A))
gedefinieerd door
=A-X)
voor alle
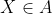
. Bewijs dat
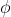
bijectief is.
Even een kleine notitie:
)
is de PowerSet, dus de verzameling van alle deelverzamelingen en
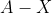
wordt in dit boek zo geschreven, maar ik noteer het liever als A\X, wat me niet lukt om in de formule te typen.
Dit is dus wat ik moet bewijzen. In de post hieronder zal ik proberen uiteen te zetten wat ik al heb.
-
Ilona
- Gevorderde

- Berichten: 100
- Lid geworden op: 13 sep 2013, 11:33
Bericht
door Ilona » 04 okt 2014, 14:02
Injectiviteit bewijzen kan door te bewijzen dat als
=\phi(y))
dat dan ook moet gelden dat
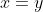
of anders gezegd:
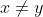
impliceert
 \neq \phi(y))
Ik dacht dit te bewijzen uit het ongerijmde: stel
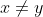
maar
=\phi(y))
dan moet ik op een tegenspraak komen. Maar op zich is dat natuurlijk heel logisch, alleen weet ik niet hoe ik dat netjes kan bewijzen. Dus daar loop ik al vast.
De surjectiviteit: voor alle
)
(codomein) moet er een
)
(domein) bestaan zodat
=b)
.
Ik zou graag iemand hebben die met me meedenkt.
-
op=op
- Vergevorderde

- Berichten: 1087
- Lid geworden op: 23 apr 2010, 18:11
Bericht
door op=op » 04 okt 2014, 21:09
Powerset? Machtsverzameling.
Surjectiviteit is lijkt me makkelijk.
Je moet dan aantonen dat voor elke deelverzameling
van

er een verzameling

is zo dat
 = X)
.
Drie keer raden wat hier voor

ingevuld moet worden.
Injectiviteit.
Stel
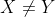
,
je moet dan aantonen dat
 \neq \phi(Y))
.
Schrijf
 \neq \phi(Y))
eens volledig uit.
-
Ilona
- Gevorderde

- Berichten: 100
- Lid geworden op: 13 sep 2013, 11:33
Bericht
door Ilona » 05 okt 2014, 12:30
Dit is wat ik nu heb. Injectief: als
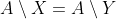
dan moet gelden
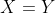
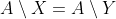
 = A \setminus (A \setminus Y))
In theorie 3.3.8 is gegeven dat
=A)
dan en slechts dan A een deelverzameling is van B. In dit geval is X een deelverzameling van A, dus geldt:
 = A \setminus (A \setminus Y) = Y)
en dus is de functie injectief.
En ik dacht dat als je B kiest als
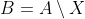
, dan
= X)
Klopt dat?
(edit: die theorie waar ik naar verwijs is van het vorige hoofdstuk en hebben we toen bewezen, dus mag ik nu gebruiken, vandaar)



