Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
JelleOlthuis
- Nieuw lid

- Berichten: 5
- Lid geworden op: 04 feb 2012, 16:23
Bericht
door JelleOlthuis » 21 okt 2015, 10:52
Hai,
voor ons tentamen wiskunde krijgen we standaard een vraag van tevoren opgegeven die dan als soort van doordenker op het tentamen komt. dit keer was het:
voor welke waarden van n geldt:
=nx^{n-1})
nu kregen we natuurlijk het antwoord er niet bij en zelf ben ik niet zeker of ik het goed heb...
ik dacht namelijk zelf aan:
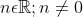
maar ben hier dus niet zeker van. graag zou ik suggesties/antwoorden/een stap in de goede richting willen hebben zodat ik iig dit punt al heb op het tentamen

-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 21 okt 2015, 12:20
Waarom zou n niet 0 mogen zijn ...
Wat is x^0?
-
JelleOlthuis
- Nieuw lid

- Berichten: 5
- Lid geworden op: 04 feb 2012, 16:23
Bericht
door JelleOlthuis » 21 okt 2015, 15:38
eigenlijk nu je het zo zet mag x=0 wel...maar hoe nu verder?
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 21 okt 2015, 15:58
Wat bedoel je ...
Welke bewijzen heb je gezien voor het bestaan van deze afgeleide ...
-
angerious
- Nieuw lid

- Berichten: 1
- Lid geworden op: 21 okt 2015, 18:22
Bericht
door angerious » 21 okt 2015, 18:30
Is dit niet gewoon voor alle waarden van n met element van R?
Als n = 0 is je afgeleide gelijk aan 0, maar nog wel in de vorm van n*x^n-1 alleen als je hem uitwerkt heb je gewoon 0, maar de afgeleide verandert niet opeens.

