Wiskundeforum

Prima! Zijn hier nog vragen over ...

Dan nu: 'het geval' f(c)<0 ...

Nee, conceptueel en algebraïsch snap ik het voor c > 0.

c < 0 is echter een ander verhaal. Aan de ene kant denk ik dat het hetzelfde is als voor c > 0, enkel moet ik nog rekening houden met een vermenigvuldiging met (-1). Ik krijg dan:


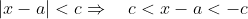
Omdat ik hier al rekening heb gehouden met het teken van c, kunnen we c > 0 beschouwen.
Ik krijg een tegenstrijdigheid, maar ik zie niet direct wat ik fout doe.

Conceptueel vind ik het al raar om bv. |x| < -3 te zeggen. I.e. een afstand die kleiner is dan een negatief getal. Volgens mij is heel die ongelijkheid dan gewoon fout.

spacebob schreef: Conceptueel vind ik het al raar om bv. |x| < -3 te zeggen. I.e. een afstand die kleiner is dan een negatief getal. Volgens mij is heel die ongelijkheid dan gewoon fout.

Nee hoor, |x|<-3 heeft geen opl, netjes gezegd: de opl verz is leeg.
Dit lijkt misschien flauw maar in de wiskunde is het belangrijk rekening te houden met de mogelijkheid van een lege verzameling.

Overigens gaat het (dacht ik) niet om c maar om f(c) ...

Verder: ga uit van f(c)<0 <=> -f(c)>0

Ik had gewoon even c genomen als voorbeeld.

SafeX schreef: Nee hoor, |x|<-3 heeft geen opl, netjes gezegd: de opl verz is leeg.

Ik begrijp dat er geen oplossingen zijn. Mijn verwarring kwam voornamelijk uit |x-a| < f(c) met f(c) < 0. Oorspronkelijk dacht ik dat het analoog zou zijn aan de situatie |x| < -3, maar dat zal waarschijnlijk niet het geval zijn omdat we nog met die 'a' zitten. Die 'a' zal voor een verschuiving zorgen waardoor we mogelijk wel een interval met oplossingen hebben. Toch?

Ik zal nog een voorbeeld geven om mijn verwarring te illustreren.

(Volgens een van mijn eerdere posts)

Als ik nu rekening hou met jouw tip f(c)<0 <=> -f(c)>0, dan krijg ik



+:= iets positiefs
-:= iets negatiefs

Het teken in het laatste deel zal afhankelijk zijn van |f(c)| < |f(a)| of andersom. Indien we in het laatste deel een positief getal hebben, dan zal dit automatisch kleiner zijn dan het getal in het eerste deel. (Volgt uit jouw tip.)

We hebben dus dit: "iets groot" < f(x) < "iets klein" met "iets kleins" < "iets groots".

Concreet als ik het toepas voor mijn bewijs:



Stel nu bv. f(c) = -2, dan krijg ik : -1 < f(x) < -3

Dat is juist het probleem in mijn bewijs.

Ik hoopte duidelijk te maken dat een ongelijkheid: |x|<-3 een lege opl verz geeft ...
Je zal dus: als f(c)<0 is, moeten werken met epsilon=-f(c)/2 (immers epsilon moet positief zijn)

SafeX schreef:Ik hoopte duidelijk te maken dat een ongelijkheid: |x|<-3 een lege opl verz geeft ...

Dat is je ook gelukt, maar ik zag gewoon niet direct hoe dat verband hield met mijn bewijs.

SafeX schreef:Je zal dus: als f(c)<0 is, moeten werken met epsilon=-f(c)/2 (immers epsilon moet positief zijn)

Ik denk dat mijn frank eindelijk gevallen is. Als ik de ongelijkheid uitwerk krijg ik:

, wat de stelling dus bewijst.


Bedankt voor je geduld en je uitleg!

Ok, succes verder!