Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
wnvl
- Vergevorderde

- Berichten: 1490
- Lid geworden op: 05 okt 2011, 16:30
Bericht
door wnvl » 01 jan 2016, 01:07
Ik kwam volgende vraag tegen
Bereken door dubbele integratie de oppervlakte van het gebied ingesloten door
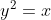
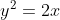
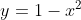
Ik kan de oppervlakte wel berekenen als ik de snijpunten van de curves bereken, dan is het op zich een eenvoudig probleem.
De snijpunten van de derde curve met de eerste 2 curves levert echter irrationale getallen waarvoor geen eenvoudige uitdrukking bestaat. Het probleem herleidt zich tot een vierde graadsvergelijking.
Mijn vraag is, zou er een slim truukje bestaan om de oppervlakte te berekenen zonder dat we de snijpunten van de curves expliciet moeten berekenen? Het betreft een examenvraag die iemand mij voorlegde en ik vermoed dat het de bedoeling is om te komen tot een exacte oplossing in een redelijke tijd zonder omslachtig rekenwerk.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 02 jan 2016, 12:22
Nee, de coördinaten van de snijpunten zijn nodig ...
-
wnvl
- Vergevorderde

- Berichten: 1490
- Lid geworden op: 05 okt 2011, 16:30
Bericht
door wnvl » 02 jan 2016, 20:41
Ja, ik dacht het ook al.
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 02 jan 2016, 20:43
Kijk eens wat je krijgt als je gebruik maakt van poolcoördinaten.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
wnvl
- Vergevorderde

- Berichten: 1490
- Lid geworden op: 05 okt 2011, 16:30
Bericht
door wnvl » 02 jan 2016, 20:59
We krijgen dan in volgorde voor mijn 3 curves
=cos(\theta))
=2 cos(\theta))
=1-r^2 \cdot cos^2(\theta))
Als je dan snijpunten gaat zoeken behoud je ook een vierdegraadsprobleem lijkt mij...
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 03 jan 2016, 11:24
wnvl schreef:We krijgen dan in volgorde voor mijn 3 curves
=cos(\theta))
=2 cos(\theta))
=1-r^2 \cdot cos^2(\theta))
Als je dan snijpunten gaat zoeken behoud je ook een vierdegraadsprobleem lijkt mij...
Schrijf iedere uitdrukking eens in de gedaante r = r(θ) en kijk eens wat dat oplevert.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 03 jan 2016, 12:45
Stel eens dat de laatste formule y = -x² zou moeten zijn, en dat er dus een fout in de opstelling van de opgave zit. Als dat zo is houd je een vierdegraadsvergelijking over die uitsluitend termen in x bevat.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
wnvl
- Vergevorderde

- Berichten: 1490
- Lid geworden op: 05 okt 2011, 16:30
Bericht
door wnvl » 03 jan 2016, 20:28
-
wnvl
- Vergevorderde

- Berichten: 1490
- Lid geworden op: 05 okt 2011, 16:30
Bericht
door wnvl » 03 jan 2016, 20:30
arno schreef:Stel eens dat de laatste formule y = -x² zou moeten zijn, en dat er dus een fout in de opstelling van de opgave zit. Als dat zo is houd je een vierdegraadsvergelijking over die uitsluitend termen in x bevat.
Bedoel je met deze opmerking dan dat volgens jou een vierdegraadsvergelijking onvermijdelijk is?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 05 jan 2016, 18:54
wnvl schreef:arno schreef:Stel eens dat de laatste formule y = -x² zou moeten zijn, en dat er dus een fout in de opstelling van de opgave zit. Als dat zo is houd je een vierdegraadsvergelijking over die uitsluitend termen in x bevat.
Bedoel je met deze opmerking dan dat volgens jou een vierdegraadsvergelijking onvermijdelijk is?
Ja, maar het is in ieder geval een vierdegraadsvergelijking die gemakkelijk door ontbinden in factoren kan worden opgelost.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel


