Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
wouter205
- Nieuw lid

- Berichten: 11
- Lid geworden op: 13 mar 2014, 11:57
Bericht
door wouter205 » 25 mei 2016, 20:47
Beste,
Ik heb hier 2 opgaves van limietberekening goniometrische functies waar ik niet zeker ben over de uitkomst:
- Lim x->0 ((x + tan x)/x) en
- lim x->0 (cos x)/x
De tweede meen ik is - en + oneindig (linkerlimiet en rechterlimiet) dus bestaat de limiet niet. Maar hoe noteer ik dit wiskundig?
Voor de eerste geraak ik niet verder dan tan x vervangen door sin x / cos x waardoor je dus 1 / 0 zou uitkomen. Klopt dit?
alvast bedankt,
wouter
-
Kinu
- Moderator

- Berichten: 1144
- Lid geworden op: 22 okt 2010, 15:38
Bericht
door Kinu » 25 mei 2016, 21:15
wouter205 schreef:Beste,
Ik heb hier 2 opgaves van limietberekening goniometrische functies waar ik niet zeker ben over de uitkomst:
- Lim x->0 ((x + tan x)/x) en
- lim x->0 (cos x)/x
De tweede meen ik is - en + oneindig (linkerlimiet en rechterlimiet) dus bestaat de limiet niet. Maar hoe noteer ik dit wiskundig?
Voor de eerste geraak ik niet verder dan tan x vervangen door sin x / cos x waardoor je dus 1 / 0 zou uitkomen. Klopt dit?
alvast bedankt,
wouter
Limiet (1): wat weet je over
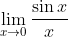
?
Limiet (2): dat klopt, de limiet bestaat niet en je moet de linker-en rechter limiet beschouwen. Qua notatie zeg je gewoon: "
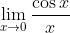
bestaat niet"
-
wouter205
- Nieuw lid

- Berichten: 11
- Lid geworden op: 13 mar 2014, 11:57
Bericht
door wouter205 » 27 mei 2016, 16:51
1) denk ondertussen gevonden te hebben:

Klopt dit? Dan snap ik wel niet de link met lim x-> 0 ((sin x)/x) (die overigens ook gelijk is aan 1
2) ok bedankt, ik noteer dit dan zo
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 27 mei 2016, 18:53
wouter205 schreef:1) denk ondertussen gevonden te hebben:

Klopt dit? Dan snap ik wel niet de link met lim x-> 0 ((sin x)/x) (die overigens ook gelijk is aan 1
2) ok bedankt, ik noteer dit dan zo
-
wouter205
- Nieuw lid

- Berichten: 11
- Lid geworden op: 13 mar 2014, 11:57
Bericht
door wouter205 » 28 mei 2016, 18:43
Ja tuurlijk, foutje van mij

de voorlaatste stap wordt dan:

sin x / x samennemen wordt 1, maar wat dan met de cos (x)?
-
Kinu
- Moderator

- Berichten: 1144
- Lid geworden op: 22 okt 2010, 15:38
Bericht
door Kinu » 02 jun 2016, 10:04
wouter205 schreef:Ja tuurlijk, foutje van mij

de voorlaatste stap wordt dan:

sin x / x samennemen wordt 1, maar wat dan met de cos (x)?
Wat weet je over

als
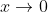
?



