Dat gaat hetzelfde als voor de raaklijn in het punt (2,8).
Alleen in plaats van x=2 neem je x=p.
Het raakpunt P op de grafiek is nu dus
)
Vervolgens gebruik je je eigen schema:
- differentieer
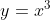
- bepaal m , door x=p in te vullen.
- Gebruik point-slope, dit levert raaklijn k in x=p:
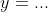
Deze lijn is nu nog uitgedrukt in p.
Welke vergelijking vind je zo?
Welke informatie hebben we in deze opgave nog meer om p te kunnen bepalen?
