Pagina 1 van 1
Ombouwen formule
Geplaatst: 08 apr 2017, 15:46
door tarfu
Hallo,
Ik wil de vergelijking (T1)^n / (p1)^n-1 = (T2)^n / (p2)^n-1 oplossen. Nu is n mijn enige onbekende. Hoe destilleer ik n uit de vergelijking?
M.vr.gr. Bob
Re: Ombouwen formule
Geplaatst: 08 apr 2017, 17:44
door arno
Bedenk dat uit
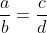
volgt dat a·d = b·c en pas dat hier eens toe.
Re: Ombouwen formule
Geplaatst: 08 apr 2017, 18:59
door SafeX
tarfu schreef:Hallo,
(T1)^n / (p1)^n-1 = (T2)^n / (p2)^n-1
Je kan dit ook schrijven als:
^n=\left(\frac{p_1}{p_2}\right)^{n-1})
Neem links en rechts de logaritme en wat levert dat op? Laat dat zien, heb je een idee om verder te kunnen?
Re: Ombouwen formule
Geplaatst: 09 apr 2017, 10:37
door tarfu
YES, ik ben eruit dankzij SafeX en mijn oude wiskundeboek df/dx van A.J. Pigmans. Graag nog even een check om te tien of het geen toevalligheid is.
n log(T1/T2) = (n-1) log(p1/p2) --> n log(T1/T2) = log(p1/p2) - log(p1/p2) -->
n log(T1/T2)-log(p1/p2) = -log(p1/p2) --> n = log(p1/p2)/(log(T1/T2)-log(p1/p2)).
In mijn geval was p1=10b, p2=1b, T1=433K en T2=300K. Ik wist dat het antwoord 1,19 moest zijn en nu weet ik het preciezer: 1,1896.
Thanks SafeX (en Pigmans

)
Re: Ombouwen formule
Geplaatst: 09 apr 2017, 13:50
door SafeX
tarfu schreef:n log(T1/T2)-log(p1/p2) = -log(p1/p2) --> n = log(p1/p2)/(log(T1/T2)-log(p1/p2)).
n(log(T1/T2)-log(p1/p2)) = -log(p1/p2) --> n = log(p1/p2)/(-log(T1/T2)+log(p1/p2)).
Ga dit na!
Re: Ombouwen formule
Geplaatst: 09 apr 2017, 14:42
door tarfu
Ik had al gemerkt dat ik vergeten wat om de n buiten haakjes te noteren al had ik er wel mee gerekend.
Het verwisselen van alle plussen in minnen geeft hetzelfde antwoord, ik snap alleen de opmerking niet. Had ik het niet goed gedaan? Ik heb beide kanten gedeeld door log(T1/T2)-log(p1/p2), daarmee wijzigen de plussen en minnen toch niet mee?
Re: Ombouwen formule
Geplaatst: 10 apr 2017, 20:40
door David
tarfu schreef:Had ik het niet goed gedaan?
Je bent goed op weg

tarfu schreef:n log(T1/T2)-log(p1/p2) = -log(p1/p2) --> n = log(p1/p2)/(log(T1/T2)-log(p1/p2)).
Laten we schrijven:
a = log(T1/T2)-log(p1/p2) en
b = log(p1/p2).
Dan heb je een vergelijking van de vorm:
a*n = -b. Hieruit volgt: n = -b/a (voor a niet 0).
Je geeft: n = b/a.