Impliciet differentiëren - Evenwijdigheid
Geplaatst: 20 okt 2017, 13:23
Beste forumleden,
Als voorbereiding op mijn tentamen was ik bezig met het oefenen van impliciet differentiëren.
Opgave:
Beschouw de kromme met vergelijking:
)
a) Bepaal de punten op de kromme, waar de raaklijn evenwijdig loopt aan de x-as
Mijn uitwerking:
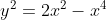
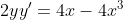 (diff. naar x) (
(diff. naar x) (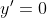 )
)
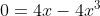 is
is )
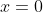
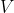
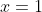
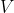
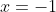
Het blijkt nu dat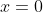 niet tot de oplossingen behoort en dit is ook heel duidelijk te zien als men de grafiek 'plot' echter heb ik deze mogelijkheid niet bij mijn tentamen.
niet tot de oplossingen behoort en dit is ook heel duidelijk te zien als men de grafiek 'plot' echter heb ik deze mogelijkheid niet bij mijn tentamen.
Mijn vraag is daarom: kan iemand mij uitleggen waaruit je kan concluderen dat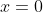 geen antwoord is op deze opgave.
geen antwoord is op deze opgave.
Alvast bedankt!
Bryan
Als voorbereiding op mijn tentamen was ik bezig met het oefenen van impliciet differentiëren.
Opgave:
Beschouw de kromme met vergelijking:
a) Bepaal de punten op de kromme, waar de raaklijn evenwijdig loopt aan de x-as
Mijn uitwerking:
Het blijkt nu dat
Mijn vraag is daarom: kan iemand mij uitleggen waaruit je kan concluderen dat
Alvast bedankt!
Bryan