Pagina 1 van 1
Oplossen limiet met een McLauren-polynoom
Geplaatst: 16 sep 2018, 12:48
door William Kl
Hallo,
Bij één van mijn examenopgaven wordt m.b.v. een McLauren polynoom een limiet bepaald, zie hieronder:

Ik snap dat de cos wordt omgeschreven naar een polynoom, maar ik begrijp niet hoe die vierde macht van deze polynoom zomaar wordt weggeschreven. Zie ik iets over het hoofd?
Alvast bedankt!
Re: Oplossen limiet met een McLauren-polynoom
Geplaatst: 16 sep 2018, 15:08
door arie
Een manier om dit te bekijken:
\right)^4)
is gelijk aan (want O(x^4) is ongevoelig voor vermenigvuldiging met -1):
\right]\right)^4)
\right]^1 + {4 \choose 2} \left[\frac{1}{2}x^2 + O(x^4)\right]^2 - {4 \choose 3} \left[\frac{1}{2}x^2 + O(x^4)\right]^3 + {4 \choose 4} \left[\frac{1}{2}x^2 + O(x^4)\right]^4)
Werk nu alleen de eerste 2 termen uit:
\right] + {4 \choose 2} \left[\frac{1}{2}x^2 + O(x^4)\right]^2 - {4 \choose 3} \left[\frac{1}{2}x^2 + O(x^4)\right]^3 + {4 \choose 4} \left[\frac{1}{2}x^2 + O(x^4)\right]^4)
 + {4 \choose 2} \left[\frac{1}{2}x^2 + O(x^4)\right]^2 - {4 \choose 3} \left[\frac{1}{2}x^2 + O(x^4)\right]^3 + {4 \choose 4} \left[\frac{1}{2}x^2 + O(x^4)\right]^4)
Alle overige termen zijn >= O(x^4), dus die vallen binnen de O(x^4) die we al hebben:
)
Wordt het hiermee duidelijker?
Re: Oplossen limiet met een McLauren-polynoom
Geplaatst: 16 sep 2018, 21:29
door William Kl
Hartelijk dank voor je antwoord!
Ik denk dat ik het begrijp, maar dan komt er bij mij toch wat anders uit (maakt overigens voor het antwoord niets uit).
)= (1-u)^4 \rightarrow u=(\frac{1}{2}x^2 + O(x^4)))
Maar als ik dan
^4)
uitschrijf kom ik tot
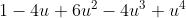
) +6(\frac{1}{2}x^2 + O(x^4))^2-4(\frac{1}{2}x^2 + O(x^4))^3+(\frac{1}{2}x^2 + O(x^4))^4)
De eerste twee en laatste termen kloppen (en de tekens voor de overige termen ook)
Doe ik hier iets wat wiskundig incorrect is?
Het uitschrijven van een 4e-orde factor heb ik nog nooit eerder zo gezien

Hoor het graag!
Re: Oplossen limiet met een McLauren-polynoom
Geplaatst: 16 sep 2018, 22:04
door arie
Dit is hetzelfde.
Ik gebruik alleen een schrijfwijze met binomiaalcoëfficiënten, zie bv.
https://en.wikipedia.org/wiki/Binomial_coefficient
Bovenaan, in de introductie, geven ze op de wiki-pagina een voorbeeld voor
^4)
.
Voor ons is dit bijna hetzelfde:
^4 = {4 \choose 0} - {4 \choose 1}u + {4 \choose 2}u^2 - {4 \choose 3}u^3 + {4 \choose 4}u^4)
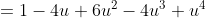
Wellicht ben je de Driehoek van Pascal (plaatje rechtsboven op die wiki pagina) al eerder tegengekomen.
Ligt hier het probleem of bedoel je iets anders?
Re: Oplossen limiet met een McLauren-polynoom
Geplaatst: 16 sep 2018, 22:30
door William Kl
Dit is volkomen nieuw voor mij, wel super interessant!
Ik kan vooruit, bedankt!
Re: Oplossen limiet met een McLauren-polynoom
Geplaatst: 17 sep 2018, 18:48
door SafeX
Kan je de limiet ook bepalen zonder de reeksontwikkeling?

