Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Integraalrekening, afgeleiden, rijen, convergentie & divergentie van reeksen, meervoudige integratie.
-
Thomke
- Nieuw lid

- Berichten: 4
- Lid geworden op: 28 jan 2019, 17:29
Bericht
door Thomke » 28 jan 2019, 17:39
Hallo allemaal. Onderstaande vergelijking doet mijn hoofd breken, iets gaat fout bij het kruislings vermenigvuldigen.
=y(x)/x)
Vervolgens zou ik zeggen
/dx=y(x)/x)
=y(x)*dx)
*dy=1/x*dx)
Waar gaat het fout?
Er moet
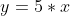
uit komen.
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 29 jan 2019, 11:43
Het gaat goed.
Merk op: je had de factor x ook rechts kunnen laten staan: deze gaat nu eerst naar links, en dan weer terug naar rechts.
De volgende stap is beide kanten integreren.
Kom je hiermee verder?
PS: voor later: in de opgave is waarschijnlijk ook een beginvoorwaarde (= initial condition) gegeven. Klopt dat?
-
Thomke
- Nieuw lid

- Berichten: 4
- Lid geworden op: 28 jan 2019, 17:29
Bericht
door Thomke » 29 jan 2019, 16:18
Ja klopt, y(1)=5, dus ik zou in eerste instantie op
=c*x)
uit moeten komen.
Als ik integreer aan beide kanten, krijg ik dan
)=ln(x)+c)
?
En hoe ik dan op
=c*x)
uit kom, geen idee..
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 29 jan 2019, 16:25
Wat krijg je als je vervolgens beide kanten als e-macht neemt?
Dus jouw gelijkheid herschrijft in de vorm:
\(e^{ln(y(x))} = e^{ln(x)+c}\)
-
Thomke
- Nieuw lid

- Berichten: 4
- Lid geworden op: 28 jan 2019, 17:29
Bericht
door Thomke » 29 jan 2019, 17:04
Ja ben alweer een stukje verder, als ik van beide kanten de e-macht neem, krijg ik e ^ ln(y(x))=e ^ ln(x)+c
-> e ^ ln(x)*e ^ c
Dit wordt dan y(x)=x*e ^ c?
Ik zit nu alleen nog met die e^c in mijn maag, dat moet eigenlijk alleen een constante worden. Kun je mij het laatste zetje geven?
-
arie
- Moderator

- Berichten: 3917
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 29 jan 2019, 17:50
Als \(c_1\) een constante is, dan is \(c_2 = e^{c_1}\) ook een constante.
Noem \(c_2\) daarna c, en je bent klaar.
-
Thomke
- Nieuw lid

- Berichten: 4
- Lid geworden op: 28 jan 2019, 17:29
Bericht
door Thomke » 30 jan 2019, 11:04
Ja, achteraf gezien is e^c op zichzelf ook een constante. Snap het nu helemaal. Bedankt!