
bewijs met volledige inductie
bewijs met volledige inductie
Onderstaande opgave is een huiswerkopgave. Echter snap ik niet hoe ik hieraan moet beginnen. Wie o wie kan mij op weg helpen?


Re: bewijs met volledige inductie
basis:
Toon aan dat de gelijkheid klopt voor n = 1
inductie:
Uitgaande van het feit dat de gelijkheid klopt voor n, moeten we aantonen dat deze ook klopt voor n+1.
We moeten dus aantonen dat
\(\sum\limits_{k=0}^n F_{2k+1} = F_{2(n+1)}-1\)
ofwel dat
\(\sum\limits_{k=0}^{n-1} F_{2k+1} + F_{2n+1} = F_{2n+2}-1\)
Gebruik nu de inductiehypothese.
Kom je hiermee verder?
Toon aan dat de gelijkheid klopt voor n = 1
inductie:
Uitgaande van het feit dat de gelijkheid klopt voor n, moeten we aantonen dat deze ook klopt voor n+1.
We moeten dus aantonen dat
\(\sum\limits_{k=0}^n F_{2k+1} = F_{2(n+1)}-1\)
ofwel dat
\(\sum\limits_{k=0}^{n-1} F_{2k+1} + F_{2n+1} = F_{2n+2}-1\)
Gebruik nu de inductiehypothese.
Kom je hiermee verder?
Re: bewijs met volledige inductie
Nee, ik kom nog niet verder. Eerst moet ik dus bewijzen dan N=1.
Hier start het probleem al. Hoe Kan ik dit bewijzen. Ik snap niet hoe ik dit moet toepassen.
Hier start het probleem al. Hoe Kan ik dit bewijzen. Ik snap niet hoe ik dit moet toepassen.
Re: bewijs met volledige inductie
Deze gelijkheid:
\(\sum\limits_{k=0}^{n-1} F_{2k+1} = F_{2n}-1\)
moeten we voor alle \(n \ge 1, n \in \mathbb{N}\) met volledige inductie bewijzen.
We bewijzen eerst dat de gelijkheid geldt voor de eerste waarde (hier n=1), dit is de basis stap.
Daarna bewijzen we dat als de gelijkheid geldt voor een willekeurig getal \(n \ge 1\), dat de gelijkheid dan ook altijd geldt voor het getal dat daarna komt, namelijk (n+1). Dit laatste is de inductieve stap.
Dus als de gelijkheid geldt voor n=1, dan geldt deze ook voor n=1+1=2,
en omdat de gelijkheid geldt voor n=2, geldt deze ook voor n=2+1=3,
en omdat de gelijkheid geldt voor n=3, geldt deze ook voor n=3+1=4, etc.
Zo door redenerend geldt de vergelijking dus voor alle \(n \ge 1, n \in \mathbb{N}\).
basis:
We moeten eerst bewijzen dat de gelijkheid klopt voor n = 1.
(voor alle duidelijkheid: we bewijzen dus niet dat n=1, maar dat de gelijkheid klopt als n gelijk aan 1 is).
Dit kan je gewoon doen door voor n de waarde 1 in te vullen.
De vergelijking wordt in dit geval:
\(\sum\limits_{k=0}^{1-1} F_{2k+1} = F_{2\cdot 1}-1\)
ofwel
\(\sum\limits_{k=0}^{0} F_{2k+1} = F_2-1\)
De sommatie links loopt van k = 0 t/m 0, dus links houden we alleen één term, namelijk die voor k=0 over.
Als k=0, welk Fibonacci getal staat er dan links?
Hoe zijn \(F_0\), \(F_1\) en \(F_2\) bij jullie gedefinieerd?
Klopt onze gelijkheid dus voor n = 1 ?
Hoe ver ben je gekomen met de inductieve stap?
\(\sum\limits_{k=0}^{n-1} F_{2k+1} = F_{2n}-1\)
moeten we voor alle \(n \ge 1, n \in \mathbb{N}\) met volledige inductie bewijzen.
We bewijzen eerst dat de gelijkheid geldt voor de eerste waarde (hier n=1), dit is de basis stap.
Daarna bewijzen we dat als de gelijkheid geldt voor een willekeurig getal \(n \ge 1\), dat de gelijkheid dan ook altijd geldt voor het getal dat daarna komt, namelijk (n+1). Dit laatste is de inductieve stap.
Dus als de gelijkheid geldt voor n=1, dan geldt deze ook voor n=1+1=2,
en omdat de gelijkheid geldt voor n=2, geldt deze ook voor n=2+1=3,
en omdat de gelijkheid geldt voor n=3, geldt deze ook voor n=3+1=4, etc.
Zo door redenerend geldt de vergelijking dus voor alle \(n \ge 1, n \in \mathbb{N}\).
basis:
We moeten eerst bewijzen dat de gelijkheid klopt voor n = 1.
(voor alle duidelijkheid: we bewijzen dus niet dat n=1, maar dat de gelijkheid klopt als n gelijk aan 1 is).
Dit kan je gewoon doen door voor n de waarde 1 in te vullen.
De vergelijking wordt in dit geval:
\(\sum\limits_{k=0}^{1-1} F_{2k+1} = F_{2\cdot 1}-1\)
ofwel
\(\sum\limits_{k=0}^{0} F_{2k+1} = F_2-1\)
De sommatie links loopt van k = 0 t/m 0, dus links houden we alleen één term, namelijk die voor k=0 over.
Als k=0, welk Fibonacci getal staat er dan links?
Hoe zijn \(F_0\), \(F_1\) en \(F_2\) bij jullie gedefinieerd?
Klopt onze gelijkheid dus voor n = 1 ?
Hoe ver ben je gekomen met de inductieve stap?
Re: bewijs met volledige inductie
Voor k=0 geldt dat dit 0 is.
Voor
F=0 ==>>0
F=1 ==>> 1
F=2 ==>> 1
Voor de rechterkant geldt dan
ook dat is dit 1 is. Door 1-1= 0
Hiermee is het bewijs geleverd voor n=1.
De inductieve stap moet ik nog verder mee gaan. Maar als het goed is begrijp ik nu de basisstap.
Voor
F=0 ==>>0
F=1 ==>> 1
F=2 ==>> 1
Voor de rechterkant geldt dan
ook dat is dit 1 is. Door 1-1= 0
Hiermee is het bewijs geleverd voor n=1.
De inductieve stap moet ik nog verder mee gaan. Maar als het goed is begrijp ik nu de basisstap.
Re: bewijs met volledige inductie
Nog wel een opmerking over de basisstap:
We hebben deze vergelijking:
\(\sum\limits_{k=0}^{n-1} F_{2k+1} = F_{2n}-1\)
Voor n=1 krijgen we zoals we hierboven al zagen:
\(\sum\limits_{k=0}^{0} F_{2k+1} = F_{2}-1\)
ofwel
\(F_{2\cdot 0+1} = F_2-1\)
ofwel
\(F_1 = F_2-1\)
Maar dit klopt alleen als
\(F_0 = 1\)
\(F_1 = 1\)
\(F_2 = F_1 + F_0 = 2\)
(vul deze getallen maar in in de vergelijking \(F_1 = F_2 - 1\))
Werken jullie wellicht met deze definitie van de Fibonacci getallen?
Met jouw definitie (\(F_0 = 0, \; F_1 = 1, \; F_2 = 1\)) is \(F_1 \neq F_2 -1\)
Deze definitie (\(F_0 = 0, \; F_1 = 1\)) is overigens wel gebruikelijker.
Nog een controle:
Neem \(F_0 = 1, \; F_1 = 1, \; F_2 = 2, \; F_3 = 3, \; F_4 = 5, \; F_5 = 8, \; F_6 = 13\),
dan levert dit in de vergelijking voor n=3:
\(\sum\limits_{k=0}^{3-1} F_{2k+1} = F_{2\cdot 3}-1\)
\(\sum\limits_{k=0}^{2} F_{2k+1} = F_6-1\)
\(F_{2\cdot 0+1} + F_{2\cdot 1+1} + F_{2\cdot 2+1} = F_6-1\)
\(F_1 + F_3 + F_5 = F_6-1\)
\(1 + 3 + 8 = 13 - 1\)
en dit klopt.
Maar met \(F_0 = 0, \; F_1 = 1, \; F_2 = 1, \; F_3 = 2, \; F_4 = 3, \; F_5 = 5, \; F_6 = 8\) staat er:
\(1 + 2 + 5 = 8 - 1\)
en dit klopt niet...
We hebben deze vergelijking:
\(\sum\limits_{k=0}^{n-1} F_{2k+1} = F_{2n}-1\)
Voor n=1 krijgen we zoals we hierboven al zagen:
\(\sum\limits_{k=0}^{0} F_{2k+1} = F_{2}-1\)
ofwel
\(F_{2\cdot 0+1} = F_2-1\)
ofwel
\(F_1 = F_2-1\)
Maar dit klopt alleen als
\(F_0 = 1\)
\(F_1 = 1\)
\(F_2 = F_1 + F_0 = 2\)
(vul deze getallen maar in in de vergelijking \(F_1 = F_2 - 1\))
Werken jullie wellicht met deze definitie van de Fibonacci getallen?
Met jouw definitie (\(F_0 = 0, \; F_1 = 1, \; F_2 = 1\)) is \(F_1 \neq F_2 -1\)
Deze definitie (\(F_0 = 0, \; F_1 = 1\)) is overigens wel gebruikelijker.
Nog een controle:
Neem \(F_0 = 1, \; F_1 = 1, \; F_2 = 2, \; F_3 = 3, \; F_4 = 5, \; F_5 = 8, \; F_6 = 13\),
dan levert dit in de vergelijking voor n=3:
\(\sum\limits_{k=0}^{3-1} F_{2k+1} = F_{2\cdot 3}-1\)
\(\sum\limits_{k=0}^{2} F_{2k+1} = F_6-1\)
\(F_{2\cdot 0+1} + F_{2\cdot 1+1} + F_{2\cdot 2+1} = F_6-1\)
\(F_1 + F_3 + F_5 = F_6-1\)
\(1 + 3 + 8 = 13 - 1\)
en dit klopt.
Maar met \(F_0 = 0, \; F_1 = 1, \; F_2 = 1, \; F_3 = 2, \; F_4 = 3, \; F_5 = 5, \; F_6 = 8\) staat er:
\(1 + 2 + 5 = 8 - 1\)
en dit klopt niet...
Re: bewijs met volledige inductie
Er is geen 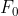 en
en 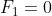 ontbrak in het gegeven van de opgave.
ontbrak in het gegeven van de opgave.

