Ah...
Een methode om hierachter te komen, is om een relatief ingewikkelde functie te bedenken, - een met veel punten waar de richting veranderd... veel toppen enzo dus... iets in de richting van
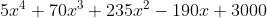
Ok, nu plot je dit...
een passend domein is: -10...4
een passend bereik is: 0..4000
Op zich wel een grappig figuur

Laten wij nu de afgeleide bepalen.

En daarvan de afgeleide?

Ok, nu hebben we wel de 1e en 2e afgeleide... maar laten wij eens logisch denken wat we kunnen beredeneren.
Aan de hand van de afgeleide kunnen we 1 ding heel snel zien: Is de grafiek stijgend, of dalend op dit punt, of blijft hij gelijk?
Situatie:
f'(x) > 0: De grafiek gaat omhoog op dit punt.
f'(x) = 0: De grafiek gaat op dit punt nog omhoog, nog omlaag. Een soort top.
f'(x) < 0: De grafiek gaat omlaag op dit punt.
Ok, dus we kunnen heel simpel een paar dingen zien. Maar, we willen meer weten. Heel vaak horen we wel van een toenemend dalende grafiek, of een toenemend stijgende grafiek. Kunnen we dit soort situaties ook herkennen aan de afgeleide?
Laten we dan eens kijken naar wat de afgeleide doet.
Als de afgeleide stijgend is, dan hebben we te maken met een grafiek, waarvan het richtingscoefficient steeds groter wordt. Als de afgeleide gelijk blijft, is de richtingscoefficient gelijk. Als de afgeleide daalt, wordt de richtingscoefficient steeds kleiner.
Maar, we hebben twee benamingen voor wanneer de rico kleiner en kleiner wordt. Afnemend stijgend, en Toenemend Dalend ( De Stijging wordt kleiner, of de Daling wordt groter )...
Maar, we hebben ook twee benamingen voor wanneer de rico groter en groter wordt. Toenemd stijgend of Afnemend Dalend ( De Stijging wordt groter, of de Daling wordt kleiner )...
Maar hoe weten we nu of de afgeleide stijgt of daalt? Tsja, daar is een trukje voor... We vergeten even dat de afgeleide de afgeleide is, en nemen ons voor even te denken dat dit de functie is die we willen bestuderen. Om het stijgen of dalen te bekijken, moeten we van deze nieuwe functie naar de afgeleide kijken. Hierdoor vinden we extra informatie.
Over het algemeen vinden we een aantal situaties:
f'(x) > 0
f''(x) > 0 : toenemend stijgend
f''(x) = 0 : constant stijgend
f''(x) < 0 : afnemend stijgend
f'(x) = 0
f''(x) > 0 : We staan nu even stil, maar straks gaan we stijgen!
f''(x) = 0 : Poe! We gaan niet stijgen en niet dalen. We kunnen erg weinig zeggen zonder de 3e afgeleide

f''(x) < 0 : We staan stil, straks gaan we dalen!
f'(x) < 0
f''(x) > 0 : afnemend dalend
f''(x) = 0 : constant dalend
f''(x) < 0 : toenemend dalend
tsja, als eerste hoop ik dat je dit begrijpt... zo niet, gebruik het dan ook niet

``Life is complex. It has real and imaginary parts.''

