Ik heb een oefening voor mij liggen om foutenbepaling te doen d.m.v. het differentiequotiënt.
Een sferische figuur (met straal: 10cm) is gevuld tot op hoogte (h). Het volume bedraagt:
pi/3(30*(h)^2 - (h)^3). Waarbij h wordt gemeten met een fout van 0,1cm en de hoogte aan vloeistof bedraagt 5,00cm.
Mijn logica:
pi/3(30*(0,1)^2 - (0,1)^3) = 0,31311 * 50 = 15,66
Volgens de differentiequotiënt wordt dit:
f'(V)= pi/3(30*2*(5) - 3*(5)^2)= 235,62 (afgerond) * 0,1 (AF) = 23,56
Als ik mijn logica van gezond boerenverstand toepas bekom ik een andere fout dan deze die bekomen wordt door het differentiequotiënt. Wat is de reden?
Wat is de logica van het differentiequotiënt?
-
Into the library...
- Nieuw lid

- Berichten: 7
- Lid geworden op: 16 jan 2013, 18:35
Re: Wat is de logica van het differentiequotiënt?
De opgave gaat over het volume V als functie van hoogte h, gegeven door:
 = \frac{\pi}{3}(3rh^2 - h^3))
waarbij in jouw geval:
r = 10
h = 5
Nu wil je weten hoe V verandert als h iets groter (of kleiner) wordt: noem dit: h +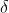 .
.
In jouw geval is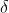 = 0.1
= 0.1
De werkelijke volumeverandering is dan:
 - V(h) = \frac{\pi}{3}(3r(h+\delta)^2 - (h+\delta)^3) - \frac{\pi}{3}(3rh^2 - h^3))
maar dit is NIET gelijk aan de
\cdot rh)
die jij berekent.
Werk zo nodig beide uitdrukkingen eens uit tot losse termen.
Concreet: in ons geval is
 - V(5) = \frac{\pi}{3}(30 \cdot 5.1^2 - 5.1^3) - \frac{\pi}{3}(30 \cdot 5^2 - 5^3)\approx 23.72)
wat goed benaderd is via de afgeleide: 23.56.
PS:
Hou je gelijkheden zuiver: het tweede gelijkteken is onjuist:
V'(h)= pi/3(30*2*(5) - 3*(5)^2)= 235,62 (afgerond) * 0,1 (AF) = 23,56
splits dit in:
V'(h)= pi/3(30*2*(5) - 3*(5)^2)= 235,62 (afgerond)
=>
V'(h) * 0,1 = 235,62 * 0,1 = 23,56 (afgerond)
waarbij in jouw geval:
r = 10
h = 5
Nu wil je weten hoe V verandert als h iets groter (of kleiner) wordt: noem dit: h +
In jouw geval is
De werkelijke volumeverandering is dan:
maar dit is NIET gelijk aan de
die jij berekent.
Werk zo nodig beide uitdrukkingen eens uit tot losse termen.
Concreet: in ons geval is
wat goed benaderd is via de afgeleide: 23.56.
PS:
Hou je gelijkheden zuiver: het tweede gelijkteken is onjuist:
V'(h)= pi/3(30*2*(5) - 3*(5)^2)= 235,62 (afgerond) * 0,1 (AF) = 23,56
splits dit in:
V'(h)= pi/3(30*2*(5) - 3*(5)^2)= 235,62 (afgerond)
=>
V'(h) * 0,1 = 235,62 * 0,1 = 23,56 (afgerond)
-
Into the library...
- Nieuw lid

- Berichten: 7
- Lid geworden op: 16 jan 2013, 18:35
Re: Wat is de logica van het differentiequotiënt?
Ik snap de logica denkelijk al. De fout die er is kan zowel positief zijn, maar ook negatief.
Dus vandaar dat ik mijn formule eerst correct dien af te leiden en daarna * AF(x)= uitkomst.
Het woord correct wil hier zeggen wat is de variabele x die men moet bepalen?
Ik denk dat de techniek die jij gebruikt niet slecht is, maar zit je met een variabele van x^7 dan is de spreiding van de uitkomst wel aanzienlijk groter dan als je dezelfde formule hebt maar dan met x^2.
Dus vandaar dat ik mijn formule eerst correct dien af te leiden en daarna * AF(x)= uitkomst.
Het woord correct wil hier zeggen wat is de variabele x die men moet bepalen?
Ik denk dat de techniek die jij gebruikt niet slecht is, maar zit je met een variabele van x^7 dan is de spreiding van de uitkomst wel aanzienlijk groter dan als je dezelfde formule hebt maar dan met x^2.
Re: Wat is de logica van het differentiequotiënt?
Die spreiding willen we juist bepalen.
Je hebt altijd een functie in de vorm y = f(x).
Verder is gegeven dat x = x0 ± delta voor een gegeven x0 en een positieve delta (= de absolute fout).
Je weet dus dat x zich tussen x0 - delta en x0 + delta bevindt:
x0 - delta < x < x0 + delta.
Aan de hand van deze grenzen van x wil je bepalen tussen welke grenzen y zich bevindt.
Aangenomen dat voor kleine delta je functie f op het interval [x0-delta, x0+delta] stijgend is, bereken je de grenzen van y via:
f(x0-delta) < y < f(x0+delta).
(indien f dalend op dit interval: pas dit laatste dan daarop aan).
Voorbeeld:
Gegeven: y = f(x) = x^7 en x=5±0.1
Dan is: f(4.9) ~= 67822 en f(5.1) ~= 89741
Gegeven de grenzen van x ligt y=f(x) dus tussen 67822 en 89741.
Deze spreiding in y wil je benaderen via de afgeleide f '(x).
Je weet:
 = \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x})
verder geldt voor een kleine (positieve) delta (= je absolute fout):
 = \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \approx \frac{f(x+\delta)-f(x)}{\delta})
dus
 \approx \frac{f(x+\delta)-f(x)}{\delta})
ofwel:
-f(x) \approx \delta \cdot f'(x))
ofwel:
 \approx f(x) + \delta \cdot f'(x))
en hier heb je je benadering van de bovengrens van y.
Evenzo voor de ondergrens.
Voorbeeld:
Terug naar bovenstaand voorbeeld, maar nu gaan we die grenzen benaderen via de afgeleide:
f(x) = x^7 dus f '(x) = 7x^6:
 \approx 5^7 + 0.1 \cdot 7 \cdot 5^6 = 89062.5)
evenzo:
 \approx 5^7 - 0.1 \cdot 7 \cdot 5^6 = 67187.5)
wat een vrij goede benadring is voor de werkelijke grenswaarden die we eerder berekend hadden:
67822 < y < 89741.
Noot: hoe kleiner delta, hoe beter deze methode werkt.
bv: f(x) = x^7 en x=5±0.01:
f(4.99) ~= 77038
f(5.01) ~= 79225
en benaderd via de afgeleide:
f(4.99) ~= f(5) - 0.01 * f '(5) ~= 77031
f(5.01) ~= f(5) + 0.01 * f '(5) ~= 79219
Reken dit zelf ook nog eens uit voor f(x)=x^7 en x=5±0.001.
Kan je verklaren waarom deze methode steeds beter klopt als de delta's kleiner worden?
Je hebt altijd een functie in de vorm y = f(x).
Verder is gegeven dat x = x0 ± delta voor een gegeven x0 en een positieve delta (= de absolute fout).
Je weet dus dat x zich tussen x0 - delta en x0 + delta bevindt:
x0 - delta < x < x0 + delta.
Aan de hand van deze grenzen van x wil je bepalen tussen welke grenzen y zich bevindt.
Aangenomen dat voor kleine delta je functie f op het interval [x0-delta, x0+delta] stijgend is, bereken je de grenzen van y via:
f(x0-delta) < y < f(x0+delta).
(indien f dalend op dit interval: pas dit laatste dan daarop aan).
Voorbeeld:
Gegeven: y = f(x) = x^7 en x=5±0.1
Dan is: f(4.9) ~= 67822 en f(5.1) ~= 89741
Gegeven de grenzen van x ligt y=f(x) dus tussen 67822 en 89741.
Deze spreiding in y wil je benaderen via de afgeleide f '(x).
Je weet:
verder geldt voor een kleine (positieve) delta (= je absolute fout):
dus
ofwel:
ofwel:
en hier heb je je benadering van de bovengrens van y.
Evenzo voor de ondergrens.
Voorbeeld:
Terug naar bovenstaand voorbeeld, maar nu gaan we die grenzen benaderen via de afgeleide:
f(x) = x^7 dus f '(x) = 7x^6:
evenzo:
wat een vrij goede benadring is voor de werkelijke grenswaarden die we eerder berekend hadden:
67822 < y < 89741.
Noot: hoe kleiner delta, hoe beter deze methode werkt.
bv: f(x) = x^7 en x=5±0.01:
f(4.99) ~= 77038
f(5.01) ~= 79225
en benaderd via de afgeleide:
f(4.99) ~= f(5) - 0.01 * f '(5) ~= 77031
f(5.01) ~= f(5) + 0.01 * f '(5) ~= 79219
Reken dit zelf ook nog eens uit voor f(x)=x^7 en x=5±0.001.
Kan je verklaren waarom deze methode steeds beter klopt als de delta's kleiner worden?
-
Into the library...
- Nieuw lid

- Berichten: 7
- Lid geworden op: 16 jan 2013, 18:35
Re: Wat is de logica van het differentiequotiënt?
De grafische definitie van het differentiequotiënt is eigenlijk niks meer dan de rico van de koorde tussen (x1,y1) en (x2,y2). Vandaar de 1. afgeleide van de functie.
De spreiding zal natuurlijk kleiner als de AF op x kleiner is, want dat willen we net bepalen. De fout op x en kijken welke impact dit heeft op de f(x).
 = x^7 - 0,001*7*5^6 = 78015,625) check:
check: 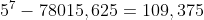
 = x^7 + 0,001*7*5^6 = 78234,375) check:
check: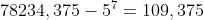
Op mijn manier krijg ik dezelfde 109,375:
*0,001 = 109,375) Maar nu als eenduidige fout en niet als spreiding tussen y - waarden.
Maar nu als eenduidige fout en niet als spreiding tussen y - waarden.
Maar dat was eigenlijk mijn vraag niet:
Stel je hebt f(x)=3*x^2-4x^2 (met x = 2 en dx = 0,4) wat is volgens jouw dan de fout?
Bereken dit opnieuw met f(x)= 3*x+4 (en dezelfde x en dx waardes, wat is dan de fout?
Doe je dit via f'(x)*dx wat bekom je dan als uitkomst bij de eerste functie en welke bij de andere functie?
Die laatste is de hoofdvraag.
De spreiding zal natuurlijk kleiner als de AF op x kleiner is, want dat willen we net bepalen. De fout op x en kijken welke impact dit heeft op de f(x).
Op mijn manier krijg ik dezelfde 109,375:
Maar dat was eigenlijk mijn vraag niet:
Stel je hebt f(x)=3*x^2-4x^2 (met x = 2 en dx = 0,4) wat is volgens jouw dan de fout?
Bereken dit opnieuw met f(x)= 3*x+4 (en dezelfde x en dx waardes, wat is dan de fout?
Doe je dit via f'(x)*dx wat bekom je dan als uitkomst bij de eerste functie en welke bij de andere functie?
Die laatste is de hoofdvraag.
Re: Wat is de logica van het differentiequotiënt?
Dit werkt net als hierboven:Into the library... schreef:...
Maar dat was eigenlijk mijn vraag niet:
Stel je hebt f(x)=3*x^2-4x^2 (met x = 2 en dx = 0,4) wat is volgens jouw dan de fout?
Bereken dit opnieuw met f(x)= 3*x+4 (en dezelfde x en dx waardes, wat is dan de fout?
Doe je dit via f'(x)*dx wat bekom je dan als uitkomst bij de eerste functie en welke bij de andere functie?
...
[geval 1]
f(x) = 3*x^2-4x^2 = -x^2
Als x = 2 ± 0.4, dus 1.6 < x < 2.4
dan is f(2.4) < f(x) < f(1.6)
ofwel -5.76 < f(x) < -2.56
ofwel f(x) = -4.16 ± 1.6
Benaderd:
f '(x) = -2x
f(2)+0.4*f '(2) < f(x) < f(2)-0.4*f '(2)
ofwel -5.6 < f(x) < -2.4
ofwel f(x) = -4 ± 1.6
[geval 2]
f(x) = 3x + 4
Als x = 2 ± 0.4, dus 1.6 < x < 2.4
dan is f(1.6) < f(x) < f(2.4)
ofwel 8.8 < f(x) < 11.2
ofwel f(x) = 10 ± 1.2
Benaderd:
f '(x) = 3
f(2)-0.4*f '(2) < f(x) < f(2)+0.4*f '(2)
ofwel 8.8 < f(x) < 11.2
ofwel f(x) = 10 ± 1.2
-
Into the library...
- Nieuw lid

- Berichten: 7
- Lid geworden op: 16 jan 2013, 18:35
Re: Wat is de logica van het differentiequotiënt?
Bedankt arie! Ik bekom dezelfde foutenmarge maar omdat ik wat sneller wou zijn heb ik f'(x)*AF(x)gedaan.
Dus: (3x^2 - 8x)*0,4 (x = 2) en dat geeft inderdaad 1,6 als absolute fout.
Maar de manier waarop jij het doet is beter omdat het meer gegevens oplevert en zo had ik het nog niet bekeken. Op naar de volgende uitdaging! (maar dat is voor morgen natuurlijk )
)
Dus: (3x^2 - 8x)*0,4 (x = 2) en dat geeft inderdaad 1,6 als absolute fout.
Maar de manier waarop jij het doet is beter omdat het meer gegevens oplevert en zo had ik het nog niet bekeken. Op naar de volgende uitdaging! (maar dat is voor morgen natuurlijk
