Pagina 1 van 1
Re: ff opfrissen
Geplaatst: 13 sep 2013, 07:10
door arie
Kijk de eerste 4 pagina's hiervan even door:
http://www.stewartcalculus.com/data/CAL ... ns_Stu.pdf
Wat is in jouw voorbeeld de karakteristieke vergelijking ?
Wat zijn daarvan de oplossingen ?
Wat is dus de algemene oplossing van je differentiaalvergelijking ?
Alternatief via bekende formules:
Voor welke bekende functies geldt dat de tweede afgeleide gelijk is aan het tegengestelde van die functies zelf ?
Kan je hiermee de algemene oplossing construeren ?
Re: ff opfrissen
Geplaatst: 14 sep 2013, 00:20
door 0AintLifeGrand0
bedankt voor je antwoord arie.
Ik mag dit probleem niet oplossen met door de karakteristieke en homogene oplossing te bepalen. Moet ' ter oefening' met integreren (zoals in het voorbeeld) of met bekende calculus trucjes.
Ik ga je link even doorbladeren, thanks
Re: ff opfrissen
Geplaatst: 14 sep 2013, 07:20
door op=op
Re: ff opfrissen
Geplaatst: 18 sep 2013, 06:13
door Sjoerd Job
0AintLifeGrand0 schreef:
Ik kan b.v. wel oplossen y'=y dat snap ik.(PS. met y is bedoeld y(x)) Dan kan ik links en rechts delen door y wat geeft:
*y'=1)
oftewel
*(dy/dx)=1)
wat leidt tot
*dy=1dx)
Nu links en rechts integreren levert
=x + C)
en door aan beide zijden e^ te verheffen levert dat:
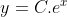
waarbij
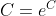
.
Ik heb echter niet echt een idee hoe ik y''=-y aan moet pakken. Hebben jullie een idee?
Aan de hand van je eigen oplossing:
*y'=-1)
oftewel
*(dy/dx)=-1)
wat leidt tot
*dy=-1dx)
Nu links en rechts integreren levert
... ga hier verder ...
Re: ff opfrissen
Geplaatst: 18 sep 2013, 13:16
door 0AintLifeGrand0
Hoi Sjoerd Job,
Je hebt 1 ding gemist...
y' = -y is geen probleem om op te lossen. Dat kan idd gewoon via de methode die ik al liet zien.
Maar de vraag was : y''=-y (tweede afgeleide, niet de eerste afgeleide).
Echter ik heb inmiddels al vernomen dat de oplossing niet met calculus behaalt hoefde te worden. Ik mocht ook kennis over differentiëren gebruiken. In dat geval is het makkelijk. Er zijn 2 functies die zichzelf negatief terug krijgen bij 2x differentieren, sin(x) en cos(x)... dus y=c2.sin(x)+c1.cos(x)...
That was all I needed to known, moeilijker hoeven we het niet te maken...