Hoi, ben zeker geen wiskundige maar zit met een ideetje, als dit al eens geopperd is, sorry voor de herhaling, als het gewoon compleet verkeerd is, ook sorry, maar toch...
√4 = 2, maar kan toch ook √4 = -2, immers:
Als √4² = -2²
<=> 4 = -2 * -2
<=> 4 = 4
Wij kiezen blijkbaar altijd het positief equivalent.
Bestaat er dan ev. geen apart symbool, vb. ¯√ (let wel, NIET -√),
waarbij de uitkomst het negatief equivalent van beide mogelijkheden is?
Men heeft dan "dezelfde" oplossing als bij de "gewone" √, maar dan als oplossing de negatieve equivalent ervan.
VOORBEELD:
¯√4 = -2 (t.o.v. √4 = 2, ¯√4 is heeft dan als negatieve equivalente oplossing -2)
¯√4² = -2²
√ valt weg door ², en het ¯ teken boven √ wordt gekwadrateerd (?): - * - = +
<=> 4 = -2 * -2
<=> 4 = 4 (vergelijking klopt)
Is er dan ook geen negatief kwadraat mogelijk? Vb. X¯² ?
I.p.v. 2 dezelfde (allebei + of -) getallen met elkaar te vermenigvuldigen, wordt in dit geval het getal vermenigvuldigd met zijn negatieve equivalent, bijna hetzelfde dus als gewoon kwadrateren, maar dan met diens negatief equivalent als oplossing?
VOORBEELD:
2¯² = 2 * -2 = -4 (i.p.v 2² = 4, 2¯² heeft dan diens negatief equivalente oplossing = -4)
Met i gaat dit ook:
√-1 = i
-1 = i²
¯√-1 = -i
( ¯√-1)² = (-i)²
-1 = i²
Indien dit mogelijk is, is het ook mogelijk om een ¯√ te maken van een negatief getal?
Waarschijnlijk niet, want:
Vb.
¯√-4 = 2 OF -2 (zoals bij de gewone √)
( ¯√-4)² = 2² ( of -2²) waarbij de √ wegvalt, en het NEGATIEVE (van ¯√) weer gekwadrateerd wordt:
-4 = 4, vergelijking klopt niet...
( ¯√-4)¯² = 2¯² waarbij de √ ook wegvalt,
MAAR het NEGATIEVE equivalent (¯²) blijft dan over:
-(-4) = 2 * -2
4 = -4, klopt dus ook niet... (maar met gewone √ en ² ging dit ook al niet)
Misschien allemaal wat simpel, maar wou toch even zien of er iets in zit...
Dank!
¯√x en x¯²
Re: ¯√x en x¯²
Heb beseft dat de negatieve wortels ¯√x idem als -√x is... Sorry!
Dit geldt ook voor ¯³√x, dit is ook -³√x
X¯² is dan ook -X², enzovoort...
Dit geldt ook voor ¯³√x, dit is ook -³√x
X¯² is dan ook -X², enzovoort...
Re: ¯√x en x¯²
Je hebt inderdaad de juiste conclusie getrokken dat de wortel uit een getal positief gekozen is en dat is een definitie.
Deze definitie is noodzakelijk want je eist natuurlijk dat bv
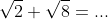
precies één antwoord oplevert ...
Verder moet je begrijpen dat het wortelteken een eenduidige definitie noodzakelijk maakt!
Deze definitie is noodzakelijk want je eist natuurlijk dat bv
precies één antwoord oplevert ...
Verder moet je begrijpen dat het wortelteken een eenduidige definitie noodzakelijk maakt!

