Ik heb geen vraag of wiskundeprobleem. Enkel wat nachtelijke gedachtenkronkels waarover ik graag wat opmerkingen had gehad van gelijk wie er iets over kan zeggen.
Mijn gedachtengang:
Je reist van punt A naar B. Afstand tussen A en B is bepaald en groter dan 0.
Stel, je start bij A op tijdstip t0. Je bereikt punt B op tijdstip t1. Hoe groter je snelheid, v, hoe eerder je aankomt bij B.
In de limiet, bij een oneindige snelheid, bereik je punt B op tijdstip t1 = t0.
Nu, fysisch is het misschien niet mogelijk, maar met welke snelheid bereik ik B voordat ik vertrek vanuit A, en dus t1 < t0?
Uit het gebruik van imaginaire getallen redeneer ik dat fysieke onmogelijkheid de wiskunde niet belet om er over na te denken. Ook dacht ik dat de complexe getallen een oplossing boden aan het probleem dat sommige wiskundige problemen niet konden worden opgelost met enkel reële getallen.
Blijkt nu dat mijn probleem ook geen oplossing heeft in de voor mij bekende getallenverzameling. Je hebt namelijk een snelheid, en dus getal, nodig groter dan oneindig. Van dit soort getallen, om het kind een naam te geven zal ik het "supergetallen" noemen, zouden er evenveel zijn (een evengrote oneindigheid) als complexe getallen. Namelijk, voor ieder punt t1 in de toekomst waarop je punt B kan bereiken, is er een punt in het verleden t2, even ver verwijderd van t0 als t1, waarop je punt B ook had kunnen bereiken.
Een nieuwe soort, niet-reële getallen dus. Of niet?
Als ik even deze vergelijking voor ogen neem:
t = x / v met t de reistijd
, zie ik dat dit "aankomen voor vertrek" simpelweg kan bereikt worden door een negatieve snelheid te nemen.
Dus, vertrekkend in A op t0, reizend met een negatieve snelheid, kom ik aan in B op tijdstip t1 met t1 < t0.
Dit lijkt me logisch op het punt na dat mijn negatieve snelheid hier dus groter schijnt te zijn dan oneindig, of gelijk welke andere positieve snelheid. Ik gebruik hier dus de negatieve getallen als eindige getallen die groter zijn dan oneindig.
Want om vroeger bij A aan te komen, heb ik een grotere snelheid nodig, groter nog dan oneindig, en dit heb ik bereikt met de negatieve getallen. Bij snelheid -5 kom ik eerder aan bij B dan met een snelheid 5, dus -5 > 5, wat natuurlijk onzin is.
Dus waarom heb ik me tot in de onzin geredeneerd? Enkele redenen die ik kan bedenken:
A. Aankomen voor je vertrekt is niet alleen fysisch onmogelijk, maar ook wiskundig. Je afvragen met welke snelheid je dit zou kunnen bereiken is dan gelijk als delen door 0. Het levert onzin op. Dit lijkt me echter onwaarschijnlijk, omdat we zelfs kunnen rekenen met de vierkantswortel van een negatief getal. Dan lijkt me reizen naar het verleden, wiskundig althans, piece of cake.
B. t = x / v is een te simpele formule. In werkelijkheid zijn die supergetallen niet gewoon negatieve getallen. Ook dit lijkt me onwaarschijnlijk, want wat zijn die getallen dan? Ik heb nog nooit gehoord van zo'n getallen, maar ik ben natuurlijk ook geen wiskundige.
C. Er zit een fout in mijn redenering. Dit lijkt me veruit de meest logische keuze. Maar waar zit die fout dan?
Iemand die iets zinnigs kan vertellen of verzinnen hierover?
Aankomen voor vertrek en supergetallen
Re: Aankomen voor vertrek en supergetallen
Of
D. Aankomen voor je vertrekt, binnen hetzelfde tijdsreferentiekader, is wiskundig onmogelijk, waardoor bovenstaande onzin is. Je kan wel aankomen voor je vertrekt, maar alleen als je ondertussen ook "reist" naar het verleden. Vanuit het tijdsreferentiekader bij vertrek kom je echter wel een positieve tijd na vertrek aan bij B.
D. Aankomen voor je vertrekt, binnen hetzelfde tijdsreferentiekader, is wiskundig onmogelijk, waardoor bovenstaande onzin is. Je kan wel aankomen voor je vertrekt, maar alleen als je ondertussen ook "reist" naar het verleden. Vanuit het tijdsreferentiekader bij vertrek kom je echter wel een positieve tijd na vertrek aan bij B.
-
ImaginaryMdA
- Nieuw lid

- Berichten: 8
- Lid geworden op: 27 jul 2011, 14:58
Re: Aankomen voor vertrek en supergetallen
Volgens mij is het eerder als je wilt aankomen in het verleden, betekent dat je er vandaan moet komen.
Aankomst en Vertrek zijn punten A(x0,t0) en B(x1,t1) en de reis is slecht een meetkundige lijn die A en B verbindt, er is dus geen soort richting. Naar het verleden reizen heeft eerder te maken met geheugen dat je op tijdstip B al hebt van op tijdstip A. Het enige verschil tussen een verplaatsing nog moeten ondergaan, en een verplaatsing al ondergaan hebben, is dat je je herinnert dat je de verplaatsing al ondergaan hebt of niet. Dus de snelheid blijft nog altijd te berekenen door (x1-x0)/(t1-t0).
Aankomst en Vertrek zijn punten A(x0,t0) en B(x1,t1) en de reis is slecht een meetkundige lijn die A en B verbindt, er is dus geen soort richting. Naar het verleden reizen heeft eerder te maken met geheugen dat je op tijdstip B al hebt van op tijdstip A. Het enige verschil tussen een verplaatsing nog moeten ondergaan, en een verplaatsing al ondergaan hebben, is dat je je herinnert dat je de verplaatsing al ondergaan hebt of niet. Dus de snelheid blijft nog altijd te berekenen door (x1-x0)/(t1-t0).
Re: Aankomen voor vertrek en supergetallen
neem nu: 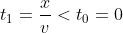 , want dat is wat je wilt.
, want dat is wat je wilt.
dus: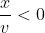 , en als v>0:
, en als v>0:
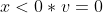 , wat niet kan, een negatieve afstand. Dus moet v wel kleiner zijn dan 0, omdat de afstand dan positief is. Logisch ook:
, wat niet kan, een negatieve afstand. Dus moet v wel kleiner zijn dan 0, omdat de afstand dan positief is. Logisch ook: 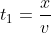 , en als t1 negatief is en x positief moet v negatief zijn. Hoe stel je je die snelheid dan voor? (neem v= -8 km/u)
, en als t1 negatief is en x positief moet v negatief zijn. Hoe stel je je die snelheid dan voor? (neem v= -8 km/u)
1: per uur ga je -8 km vooruit. Niet logisch, dan ga je gewoon achteruit, dus:
2: per -uur ga je 8 km vooruit. Dus per uur terug in de tijd ga je 8 km vooruit, of per 8 km vooruit ga je 1 uur terug in de tijd. Dit is onlogisch genoeg dat het aannemelijk lijkt. De snelheid zou je dus inderdaad gewoon negatief kunnen voorstellen.
dus:
1: per uur ga je -8 km vooruit. Niet logisch, dan ga je gewoon achteruit, dus:
2: per -uur ga je 8 km vooruit. Dus per uur terug in de tijd ga je 8 km vooruit, of per 8 km vooruit ga je 1 uur terug in de tijd. Dit is onlogisch genoeg dat het aannemelijk lijkt. De snelheid zou je dus inderdaad gewoon negatief kunnen voorstellen.
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.
Re: Aankomen voor vertrek en supergetallen
Als je volgens de speciale relativiteitstheorie sneller beweegt dan de lichtsnelheid, kan je eerder aankomen dan je vertrokken bent.
http://nl.wikipedia.org/wiki/Speciale_r ... itstheorie
http://nl.wikipedia.org/wiki/Speciale_r ... itstheorie


