Wiskundeforum

Zie ook viewtopic.php?f=15&t=3714.

De bol in hogere dimensies is zeer uitgebreid onderzocht, en daar is momenteel enorm veel over te vertellen. Het is een studieobject van de differentiaalmeetkunde.

De tabel tot nu toe is:

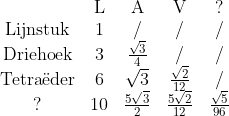
$\begin{matrix} & \text{L} & \text{A} & \text{V} & \text{?} \\ \text{Lijnstuk} & 1 & / & / & / \\ \text{Driehoek} & 3 & \frac{\sqrt{3}}{4} & / & / \\ \text{Tetra\"eder} & 6 & \sqrt{3} & \frac{\sqrt{2}}{12} & / \\ \text{?} & 10 & \frac{5\sqrt{3}}{2} & \frac{5\sqrt{2}}{12} & \frac{\sqrt{5}}{96}\end{matrix}$

Je kunt de bovenste diagonaal een beetje kunstig omvormen:
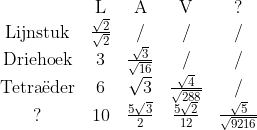
$\begin{matrix} & \text{L} & \text{A} & \text{V} & \text{?} \\ \text{Lijnstuk} & \frac{\sqrt{2}}{\sqrt{2}} & / & / & / \\ \text{Driehoek} & 3 & \frac{\sqrt{3}}{\sqrt{16}} & / & / \\ \text{Tetra\"eder} & 6 & \sqrt{3} & \frac{\sqrt{4}}{\sqrt{288}} & / \\ \text{?} & 10 & \frac{5\sqrt{3}}{2} & \frac{5\sqrt{2}}{12} & \frac{\sqrt{5}}{\sqrt{9216}}\end{matrix}$

En die lijkt te evolueren naar een quotiënt met rij A055546 in OEIS, (-1, 2, -16, 288, -9216,...) en die heeft wel iets te maken met determinanten. (Hier spreekt men zelfs over dimensies en maatgetallen voor simplexen!) Als je aanneemt dat het inderdaad die rij is, kunnen we onze tabel nog verder aanvullen:
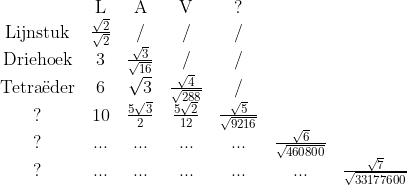
$\begin{matrix} & \text{L} & \text{A} & \text{V} & \text{?} \\ \text{Lijnstuk} & \frac{\sqrt{2}}{\sqrt{2}} & / & / & / \\ \text{Driehoek} & 3 & \frac{\sqrt{3}}{\sqrt{16}} & / & / \\ \text{Tetra\"eder} & 6 & \sqrt{3} & \frac{\sqrt{4}}{\sqrt{288}} & / \\ \text{?} & 10 & \frac{5\sqrt{3}}{2} & \frac{5\sqrt{2}}{12} & \frac{\sqrt{5}}{\sqrt{9216}}\\ ?&...&...&...&...&\frac{\sqrt{6}}{\sqrt{460800}}\\ ?&...&...&...&...&...&\frac{\sqrt{7}}{\sqrt{33177600}}\end{matrix}$

Misschien zijn er nog wel omvormingen te ontdekken voor de andere diagonalen (of zelfs in het algemeen)...

Ben nieuwsgierig naar een zinvolle definitie van negatieve dimensies.

Rationale definities zijn al wel gedefinieerd en niet zo moeilijk te begrijpen.

http://home.hccnet.nl/s.f.boukes/fractals/fracmatd.htm

Leuke vraag is, is het mogelijk het equivalent van een sfeer in een ruimte met gebroken dimensies te bepalen?.

Ik heb ook even de vijfdimensionale simplex bepaald:
$A\left(0,0,0,0,0\right);\\B\left(1,0,0,0,0\right);\\C\left(\frac{1}{2},\frac{\sqrt{3}}{2},0,0,0\right);\\D\left(\frac{1}{2},\frac{1}{2\sqrt{3}},\frac{\sqrt{2}}{\sqrt{3}},0,0\right);\\E\left(\frac{1}{2},\frac{1}{2\sqrt{3}},\frac{\sqrt{2}}{4\sqrt{3}},\frac{\sqrt{5}}{2\sqrt{2}},0\right);\\F\left(\frac{1}{2},\frac{1}{2\sqrt{3}},\frac{\sqrt{2}}{4\sqrt{3}},\frac{1}{2\sqrt{10}},\frac{\sqrt{3}}{\sqrt{5}}\right);$

En ik zag er duidelijk enkele patronen in verschijnen.
Uiteraard neem ik lengte van de zijden 1.
Een volgende simplex ontstaat door eerst het middelpunt van de vorige te bepalen:
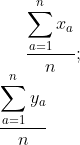
$\frac{\displaystyle\sum_{a=1}^{n}x_a}{n};\\\frac{\displaystyle\sum_{a=1}^{n}y_a}{n}$

En zo ook voor z, u, v, .... Daardoor blijven de eerste n-2 coördinaten gelijk, en de (n-1)-de wordt gedeeld door n.
Daarna bereken ik de laatste coördinaat van het laatste punt door te stellen dat de afstand tussen het laatste en het voorlaatste 1 is.

Ik schreef de n-de coördinaat dat bij de n-dimensionale simplex erbij komt eens wat anders:
Voor A: niks

voor B: $1=\frac{\sqrt{2}}{\sqrt{2}}$

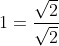
Voor C: $\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{\sqrt{4}}$

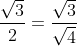
Voor D: $\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{4}}{\sqrt{6}}$

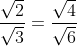
Voor E: $\frac{\sqrt{2}}{2\sqrt{2}}=\frac{\sqrt{5}}{\sqrt{8}}$

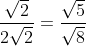
En voor F: $\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{6}}{\sqrt{10}}$

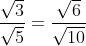
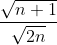
Dit geeft algemeen: $\frac{\sqrt{n+1}}{\sqrt{2n}}$ , wat gemakkelijk bewezen kan worden.

De andere coördinaatgetallen moeten gedeeld worden door n-1:
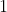
$1$ wordt $\frac{1}{2}$

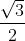
$\frac{\sqrt{3}}{2}$ wordt $\frac{\frac{\sqrt{3}}{2}}{3}=\frac{1}{2\sqrt{3}}$

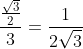
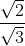
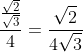
$\frac{\sqrt{2}}{\sqrt{3}}$ wordt $\frac{\frac{\sqrt{2}}{\sqrt{3}}}{4}=\frac{\sqrt{2}}{4\sqrt{3}}$
En ga maar door...

En zo kun je dus eenvoudig de coördinaten van het nieuwe punt van elke n-dimensionele simplex bepalen, namelijk gewoon
$\left(\frac{1}{2},\frac{1}{2\sqrt{3}},\frac{\sqrt{2}}{4\sqrt{3}},......,\frac{\sqrt{n}}{n\sqrt{2n-2}},\left|\frac{\sqrt{n+1}}{\sqrt{2n}}\right)$

Die laatste staat wat gescheiden omdat hij pas in de (n+1)-de dimensie aan het patroon, die wordt nog niet gedeeld door n+1.

Nu kunnen we waarschijnlijk onze tabel in het algemeen aanvullen, omdat alle coördinaten algemeen bekend zijn.

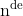
Voor n dimensies is de $\text{n}^{\text{de}}$ eenheid:

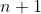
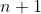
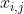
De matrix heeft dimesie $n+1$ x $n+1$ , en iedere $x_{i,j}$ is onbelangrijk voor de waarde van de determinant.

$\frac{1}{n!}*\begin{vmatrix}0 & 0 & 0 & \cdots & 0 & 0 & 1 \\\frac{\sqrt{(1)+1}}{\sqrt{2(1)}}=1 & 0 & 0 & \cdots & 0 & 0 & 1 \\x_{3,1} & \frac{\sqrt{(2)+1}}{\sqrt{2(2)}}=\frac{\sqrt{3}}{2} & 0 & \cdots & 0 & 0 & 1 \\\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\x_{n-1,1} & x_{n-1,2} & x_{n-1,3} & \cdots & 0 & 0 & 1\\x_{n,1} & x_{n,2} & x_{n,3} & \cdots & \frac{\sqrt{(n-1)+1}}{\sqrt{2(n-1)}} & 0 & 1\\x_{n+1,1} & x_{n+1,2} & x_{n+1,3} & \cdots &x_{n+1,n-1} & \frac{\sqrt{n+1}}{\sqrt{2n}} & 1 \end{vmatrix}= \prod_{k=1}^{n}(\frac{\sqrt{k+1}}{k\sqrt{2k}})$

Nu kan de tabel voor de $\text{(<n)}^{\text{de}}$ eenheden ook zeer eenvoudig aangevuld worden via
$\begin{matrix}\text{object}&\text{0 D's}&\text{1 D's}&\text{2 D's}&\text{3 D's} &\text{4 D's}&\cdots\\ \hline \text{0 D}&1&0&0&0&0&0\\ \text{1 D}&2&1&0&0&0&0\\ \text{2 D}&3&3&1&0&0&0\\ \text{3 D}&4&6&4&1&0&0\\ \text{4 D}&5&10&10&5&1&0\\ \vdots \text{ D} & \vdots & \vdots & \vdots & \vdots & \ddots & \ddots \end{matrix}$

$\prod_{k=1}^{n}\frac{\sqrt{k+1}}{k\sqrt{2k}}=\frac{1}{\sqrt{2^n}*n!*\sqrt{n!}}*\prod_{k=1}^{n}\sqrt{k+1}=\frac{1}{\sqrt{2^n}*n!*\sqrt{n!}}*\sqrt{\prod_{k=1}^{n}k+1}=\frac{1}{\sqrt{2^n}*n!*\sqrt{n!}}*\sqrt{\left(n+1\right)!}=\frac{1}{\sqrt{2^n}*n!*\sqrt{n!}}*\sqrt{n!}*\sqrt{n+1}{\color{Red} =\frac{1}{n!}*\sqrt{\frac{n+1}{2^n}}}$

Voor n=1 geeft dit 1.

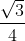
Voor n=2 geeft het $\frac{\sqrt{3}}{4}$ , klopt.

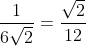
Voor n=3 is het $\frac{1}{6\sqrt{2}}=\frac{\sqrt{2}}{12}$ , en dat hadden we ook.

Voor n=4 : $\frac{\sqrt{5}}{96}$

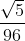
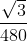
Voor n=5 : $\frac{\sqrt{3}}{480}$ , merk trouwens op dat 480² * 2 = 460800, uit rij A055546.

Dus we hebben het goed!

barto schreef:Het kan ook interessant zijn om de dimensies uit te breiden naar onder.
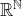
Dus van $\mathbb{R}^\mathbb{N}$ naar $\mathbb{R}^\mathbb{Z}$ .
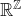
Maar ik kan nog niet direct een betekenis geven aan de -1de dimensie

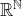
Maar wat is de `lengte' van $(1,1,\ldots)$ ? Dus $\mathbb{R}^\mathbb{N}$ is al een vreemde uitbreiding!

Ideetje voor de -1 de dimensie, naar analogie uiteraard.
Zoals je naar volgende dimensies toe steeds punten 'vervangt' door rechten en dus een extra coördinaat geeft, vervang je rechten door punten en haal je een coördinaat weg. Het probleem is wel dat je in de nulde dimensie alleen over een punt beschikt.
Dus mijn voorstel is dit:
Eigenlijk heeft het nulde-dimensie-punt 1 coördinaat dat we niet schrijven en is het punt dus een rechte dat we (terug) gaan omvormen tot punt bij overgang naar de -1de. (naar analogie met 'een punt wordt een rechte bij overgang naar hogere dimensie')
Praktisch nut en visualisatie blijven nog even achterwege

Eentje die wat inlevingsvermogen vereist:
Je hebt een hyperkubus en wil er 17 congruente hyperbollen in krijgen (in vier dimensies).
Wat is de maximale straal dat de bollen kunnen hebben?

Stel de hyperkubus heeft zijde 1, dus de ruimte die het inneemt is 1.
17 hyperbollen met straal r, vullen een ruimte van $17*\frac{1}{2}\pi^2r^4$
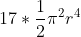
dus:
$17*\frac{1}{2}\pi^2r^4 < 1$
$r < \sqrt[4]{\frac{2}{17\pi^2}}\approx 0.33042$
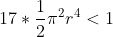
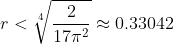
De straal moet dus kleiner zijn, wat precies, wordt nog aan gewerkt.

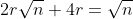
Als je eerst in 2,3 dimensies werkt (met 2²+1,2³+1 cirkelsimplexen in hun bijbehorende vierkantsimplex) vind je al snel dat $2r\sqrt n+4r=\sqrt n$ in n dimensies als de vierkantsimplex zijde 1 heeft, door de inwendigste diagonaal te beschouwen.
(De optimale schikking is uiteraard 1 in het midden, de rest aan de 'rand'.)
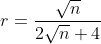
En we krijgen $r=\frac{\sqrt n}{2\sqrt n+4}$ . Een formule als een ander, of toch niet ???
in 4 dimensies is r=0,25! Dat betekent dat twee hyperbollen die aan de rand naast elkaar zitten, mekaar toch raken!
En als n=5 wordt het nog erger, ze komen dichter bij elkaar dan raken. Klopt er dan iets niet met die formule of bestaat er meer dan raken, snijden en kruisen?

En hier nog een dimensie-raadseltje:
Je beschikt over een 4D-blokje kaas K, gedefinieerd als $K=\{(x,y,z,u)|x,y,z,u\in[0;1]\}$ in het cartesisch xyzu-assenstelsel. Als we het bloke snijden volgens de 6 ruimtes x=y,x=z,x=u,y=z,y=u,z=u, hoeveel 4D-stukjes zijn er dan als we het blokje uiteenhalen?
En algemeen, wat als we een n-dimensionaal blokje snijden volgens de (n(n-1)/2) (n-1)D-ruimtes, hoeveel nD-ruimtes zijn er dan?

barto schreef:...(met 2²+1,3³+1 cirkelsimplexen in hun bijbehorende vierkantsimplex)...

moet het niet "2²+1,2³+1" zijn?

Je bent te snel, ik was nog volop aan het na-editen

(zie vorige post)

barto schreef:En hier nog een dimensie-raadseltje:
Je beschikt over een 4D-blokje kaas K, gedefinieerd als $K=\{(x,y,z,u)|x,y,z,u\in[0;1]\}$ in het cartesisch xyzu-assenstelsel. Als we het bloke snijden volgens de 6 ruimtes x=y,x=z,x=u,y=z,y=u,z=u, hoeveel 4D-stukjes zijn er dan als we het blokje uiteenhalen?
En algemeen, wat als we een n-dimensionaal blokje snijden volgens de (n(n-1)/2) (n-1)D-ruimtes, hoeveel nD-ruimtes zijn er dan?

Gezien de overvloed aan reacties zal ik maar een hint geven:

Door volgens de (n-1)-ruimte x=y te snijden, splits je de n-ruimte in twee delen: een deel met x>y en een deel met x<y.
En dan het vervolg:
wat als je slechts volgens k van de n(n-1)/2 mogelijke (n-1)-ruimtes snijdt: hoeveel n-ruimtes heb je na het blokje kaas uiteen te halen? (met 0<= 2k <= n²-n )

Je verdeelt de n-ruimte in x<y en y<x.
Zo ook in z<x en x<z, enz.
Het gaat dus om het aantal mogelijke rangschikkingen van klein naar groot van u1,u2,...,un, en dat zijn er precies n! .
bvb, voor n=2 wordt het vierkant inderdaad verdeeld in 2 delen, en de kubus (VWO 1986-1987 ronde 2 vraag 27) in 6.

Nu nog bedenken wat het wordt als we een aantal snijruimtes weglaten...

Wiskundeforum

Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?

Re: Op naar volgende dimensies via analogie?