1=0 ?!?
Geplaatst: 14 okt 2012, 16:27
Hoi!
Ik ben nieuw op dit forum en heb me aangemeld omdat ik de volgende vraag had:
Bij de zgn. Identiteit van Euler) kwam ik er via enige bewerkingen achter dat 1 (en via verdere bewerking zelfs elk reël getal) gelijk aan 0 is. Waarschijnlijk heb ik de fout gemaakt door enige operaties die voor de reële getallen wel mogen gedaan worden, te doen voor complexe getallen. Kan iemand mij dus misschien vertellen wat er hier misgegaan is???
kwam ik er via enige bewerkingen achter dat 1 (en via verdere bewerking zelfs elk reël getal) gelijk aan 0 is. Waarschijnlijk heb ik de fout gemaakt door enige operaties die voor de reële getallen wel mogen gedaan worden, te doen voor complexe getallen. Kan iemand mij dus misschien vertellen wat er hier misgegaan is???
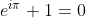
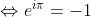
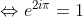 (de voorgaande vergelijking is dus gekwadrateerd)
(de voorgaande vergelijking is dus gekwadrateerd)
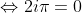 (Resultaat van de natuurlijke logaritme op beide zijden toepassen, volgens mij gaat het hier dus fout)
(Resultaat van de natuurlijke logaritme op beide zijden toepassen, volgens mij gaat het hier dus fout)
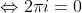
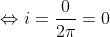
Er blijkt dus dat i gelijk aan 0 is, maar i is toch de wortel van -1??? Dit betekent dus dat:
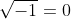
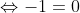 (beide kanten zijn gekwadrateerd)
(beide kanten zijn gekwadrateerd)
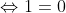 (beide kanten zijn nogmaals gekwadrateerd)
(beide kanten zijn nogmaals gekwadrateerd)
Ik was dit gisteravond tot ontdekking gekomen door wat te "spelen" met deze vergelijking en vond dit zo raar dat ik er zelf geen oplossing voor kon vinden.
Misschien dat jullie een logische verklaring kunnen geven?
Met vriendelijke groet,
Bas
Ik ben nieuw op dit forum en heb me aangemeld omdat ik de volgende vraag had:
Bij de zgn. Identiteit van Euler
Er blijkt dus dat i gelijk aan 0 is, maar i is toch de wortel van -1??? Dit betekent dus dat:
Ik was dit gisteravond tot ontdekking gekomen door wat te "spelen" met deze vergelijking en vond dit zo raar dat ik er zelf geen oplossing voor kon vinden.
Misschien dat jullie een logische verklaring kunnen geven?
Met vriendelijke groet,
Bas