Wat je dus nodig hebt is de kansdichtheidsfunctie
)
van de prijs voor een rit X.
Als je N ritten maakt wordt de verdeling van de prijs van de N ritten tesamen
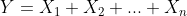
gegeven door
=f_X(x)*f_X(x)*...*f_X(x))
met * de convolutie.
De kans op een bepaald aantal ritten kan vermoedelijk gemodelleerd worden met een Poisson of Bernouilli verdeling met
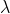
het verwacht aantal ritten per tijdseenheid. De kans op n ritten stellen we voor door P(n, t) met t de resterende looptijd van de rittenkaart.
We moeten nu over de verschillende kansen heen de verwachtte kostprijs berekenen van de nog te maken ritten voor 2 gevallen:
A: voor de huidige rit de rittenkaart gebruikt wordt, we noemen deze kost
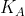
B: voor de huidige rit de rittenkaart NIET gebruikt wordt, we noemen deze kost
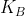
De 2 kosten moeten vergeleken worden en er moet gekozen worden voor de laagste verwachtte kost.
Bij deze oefening beschouwen we de kost van de rittenkaart 0 als die op het moment van de beslissing al gekocht is.
We berekenen de kostprijs voor A. We lopen hierbij over de kans dat er nadien nog
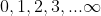
ritten volgen.
\cdot0 + P(1) \cdot E(1, t) + P(1) \cdot E(2, t) + ...)
met E(1, t) de verwachtte kosprijs van 1 rit in de nog lopende tijd t en E(2) de verwachtte kosprijs van 1 rit in de nog lopende tijd t. Die E(1, t) en E(2, t) zijn niet evident om te berekenen, want afhankelijk wanneer die ene of 2 ritten vallen zal er op dat moment voor gekozen worden om al dan niet de rittenkaart te gebruiken. Er is hier afhankelijkheid van de looptijd van de 10 rittenkaart voor E(i, t).
Ik begin de complexiteit te zien en het wordt duidelijk dat als er niet gediscretiseerd wordt, ik het niet opgelost krijg.
Als het gediscretiseerd wordt kan het m.i. opgelost worden met de technieken uit het dynamisch programmeren.



