Wiskundeforum

Een positief getal uit 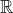is bijvoorbeeld
3,14159... .
Het bestaat uit eindig veel cijfers vóór de komma en (on)eindig veel er achter.
Laten we het eens omdraaien.
Een getal uit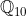 is bijvoorbeeld
...95141,3
Het bestaat uit (on)eindig veel cijfers vóór de komma en eindig veel er achter.

De positieve getallen met eindig veel cijfers vóór en achter de komma hebben i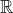n en 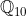dezelfde betekenis.
In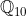 gebruiken we dezelfde rekenregels als in .

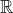...99999 + 1 = 0 (ga na!).
Blijkbaar is ...999 = -1.
...9999998 + 2 = 0
dus ...99999998 = -2.

Hoe schrijf ik 1/3 in ?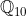
3 x ...6666667 = 1 (ga na!),
dus .6666667 = 1/3.

?
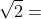We proberen ...dcba x ...dcba = 2.
Helaas geen oplossing mogelijk (ga na!).
Dus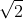 bestaat niet in .

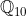en om het nog erger te maken:
...1073741824 x ...5478515625 = 0. (nuldelers)

Om nuldelers te voorkomen worden getallen niet in het tientallig stelsel bekeken, maar in p-tallige stelsels (p een priemgetal).

b.v. in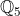 is
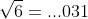en
,
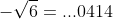want dit zijn de oplossingen van de vergelijking
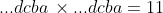(11 = 1x5 + 1).

In :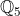
...1212 x ...1212 = ...4444 = -1.
Dus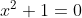 heeft een oplossing in .
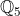Blijkbaar bevat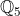 ook "".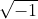

De getallen uit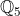 hebben heel merkwaardige eigenschappen.
Dat is dan iets voor de volgende keer.

De vergelijking heeft maar liefst 4 veschillende oplossingen in . (De oplossingen laat ik aan de lezer over).

Als , dan is .
Het maakt dus een groot verschil in wel tallig stelsel je de getallen noteert.
Voor maakt dat helemaal niets uit.

Net als in geldt, dat je een breuk (rationaal getal) kunt herkennen aan een repeterend stuk.
Dus ...1212121212 is een breuk (welke?).
Je kunt ook aan het getal (zeg X) herkennen of de breuk negatief is.
Vul daartoe eventueel wat nullen toe voor aan het getal (verschuif de komma) zodat het niet repeterende stuk r even lang is als een repeterend stuk a. Er geldt: X>0 als r>a en omgekeerd.



Hoe meer decimalen je uitrekent, hoe nauwkeuriger je benadert.

Hetzelfde geldt in (We kiezen hier n=10, maar we mogen ook een andere waarde voor n kiezen).
Absolute waarden hebben hier echter een andere betekenis dan in .
Aan de hand van 2 voorbeelden wordt het duidelijk.

Deze som begint met , dan is
.


Deze som begint met , dan is
.



Hoe meer decimalen je uitrekent, hoe nauwkeuriger je benadert.

Getallen zonder komma worden gehele getallen genoemd (dus ook ...21212 is een geheel getal). We schrijven voor de verzameling van gehele decimale getallen .

Het blijft allemaal spielerei zolang er geen toepassingen zijn. Dus tijd voor een toepassing.
Stelling van Hasse-Minkowski:
Een homogeen polynoom in n variabelen met coëfficienten in heeft nulpunten in dan en slechts dan als het nulpunten heeft in en in
voor elk priemgetal p.

Kortom, als je bijvoorbeeld kunt aantonen dat geen nulpunten heeft in ,
dan heeft de vergelijking geen oplossingen in .

Voor wie thuis is in topologie nog de volgende losse opmerkingen:
Als p priem is, dan is een lichaam.
is per definitie de completering van . We gebruiken hier de absolute-waarde metriek.
Volgens Archimedes geldt voor dat er een natuurlijk getal n bestaat zo dat .
is per definitie de completering van . We gebruiken hier de p-absolute-waarde metriek.
Archimedes geldt hier niet!
Dit zijn de enige mogelijke completeringen van met een absolute waarde begrip (i.e. een norm |.| met de eigenschap ).

De natuurlijke getallen liggen dicht in .
is compact.
Alle bollen zijn zowel open als gesloten.
Elk punt van een bol is tevens het middelpunt van die bol (bollen bevatten meerdere punten).
In elke driehoek zijn 2 zijden gelijk en de derde is kleiner.

Een reeks convergeert als de limiet van de termen naar 0 convergeert.
is homeomorf met de Cantor set.

Voor een machtreeks geldt
net als in , de formule voor de convergentiestraal.
De twee bekendste:

heeft convergentiestraal 1.
.
Vreemd genoeg is hier de convergentiestraal .
De gebruikelijke relaties gelden, zoals en enz.
Met p-adische getallen kun je dus net zo analyse bedrijven als met de reële getallen.

Een laatste opmerking:
De p-adische getallen zijn de niet-archimedische completeringen van .
We hoeven niet per sé uit te gaan van , maar kunnen in theorie ook andere niet-volledig lichamen niet-archimedisch completeren.
Die lichamen worden als uitgangspunt genomen in de niet-archimedische functionaal analyse.

Aangezien ikzelf bezig ben met een scriptie omtrent de p-adische getallen, trok deze titel mijn aandacht. Ik dacht: Interessant!

Maar, ik vond de uitwerking zelf nogal ietwat spijtig. is namelijk geen absolute waarde. Ook zou dit best benaderd mogen worden vanuit de `abstracte' weg, naast de `algebraische' weg. Laat zien wat een completering is, en dergelijke.

Tevens, waarom niet , ipv . Zo maak je duidelijk dat het om de verzameling reele getallen gaat. Ook de norm beter definieren zou denk ik goed zijn.

Sorry voor de enkele opmerkingen. Over het algemeen is het een interessant onderwerp, en ik hoop ook dat dit de interesse van mensen mag wekken.

Ik ben het geheel met je oneens.
De bedoeling van dit artikel is louter recreatief.
Als je een abstract exposé wilt moet je er een boek bij pakken.
En als ik ga uitleggen wat een completering is haakt iedere lezer af.

@ Sjoerd Job:
Ik heb op je suggestie door vervangen enz.
Een rigoreuze behandeling van het onderwerp met goede onderbouwing heeft mijn voorkeur, maar ligt voor een eerste kennismaking te zwaar op de maag.
Maar wat let je je verslag t.z.t. op deze site te publiceren.

Wanneer ik deze af heb, zal ik er over nadenken om hem hier te publiceren. Ik weet zo snel niet wat de regels hieromtrent zijn, maar als het mogelijk is, zal ik het doen.

Tevens, een rigoreuze behandeling is inderdaad iets te ver voor een `eerste kennismaking', zeker wanneer men geen rigoreuze kennismaking heeft gehad met .

Misschien is dat wel een leuk gedeelte om toe te voegen voor de wat dieper geintresseerden, een gedeelte waar rigoreuze(re) wiskunde word bedreven. Bijvoorbeeld het hele standaard regeltje



heeft een niet al te moeilijk bewijs, maar niemand die dat tegenkomt in het voortgezet onderwijs.

Als je het begrip completering al wenst te bespreken zul je eerst de begrippen convergentie van een rij en fundamentaalrij (of Cauchyrij) moeten bespreken, maar als je dit op een handige manier aanpakt moet dit volgens mij haalbaar zijn. Wiskundige begrippen zijn uiteraard uiterst abstract, maar dit hoeft naar mijn idee geen belemmering te zijn om ze hier bespreekbaar te maken.