De vergelijking
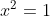
heeft 2 nulpunten, namelijk 1 en -1.
Veronderstel dat de vergelijking nog een derde oplossing heeft
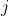
.
Dan is dus
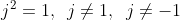
.
Met dit extra "getal" kunnen we de reële getallen uitbreiden tot de verzameling
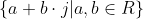
.
Getallen uit deze verzameling kun je bij elkaar optellen of met elkaar vermenigvuldigen.
Bijvoorbeeld:
(2+5\cdot j) = 6 + 19\cdot j + 10 j^2 = 16 + 19j)
.
Als
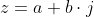
, met

en
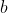
reële getallen,
dan definiëren we
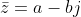
.
We definiëren nu de absolute waarde van een getal:
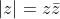
Met
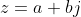
betekent dit
(a-bj) = a^2-b^2)
.
Het volgende getal heeft onze bijzondere aandacht:
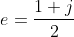
Elk getal kun je nu schrijven in de vorm
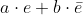
.
Kijk maar:
e + (x+y)\bar{e})
.
Dus onze getallenverzameling kunnen we ook als volgt noteren
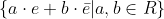
.
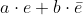
wordt meestal afgekort tot
)
.
Nu geldt
 + (c,d) = (a+c,b+d))
en
\cdot(c,d) = (ac,bd))
.
Optellen en vermenigvuldigen gaat dus coördinaatsgewijs.
De coördinaten zijn onafhankelijk van elkaar bij rekenkundige bewerkingen.
Je rekent dus als het ware met 2 onafhankelijke getallenlijnen naast elkaar.
} = (b,a))
.
| = ab)
.
Merk op:
| = 0)
dan en slechts dan als
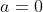
of
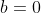
.
Dat zijn precies de getallenparen op de x-as en de y-as.
Merk ook op, voor
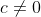
:
| = c)
dan en slechts dan als
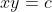
.
In woorden staat hier: De punten die op een constante afstand c van de oorsprong liggen zijn de punten op een hyperbool.
We hebben hier blijkbaar de meetkunde van voorheen te pakken.
Wat de complexe getallen zijn voor de gewone ruimte (vergelijking cirkel: |z|=c), zijn de hier besproken hyperbolische getallen voor de hyperbolische ruimte (vergelijking hyperbool: |z|=c).
Vergelijking van Euler:
 + j\sinh(\theta))
(hier is e=2,718...)
(volgt makkelijk uit machtreeksen).
We kunnen hyperbolische getallen derhalve schrijven in de vorm
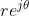
.
Zoals we complexe getallen konden inzetten om meetkundige problemen op te lossen, zo kunnen we hyperbolische getallen (ook motoren genoemd) inzetten om hyperbolisch meetkundige problemen op te lossen.
Een laatste opmerking:
Als we in
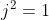
aan beide zijden de wortel trekken, dan krijgen we
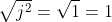
.
Blijkbaar is
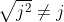
.
Stel nu dat
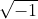
een betekenis heeft,
dan volgt uit
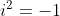
dat (aan beide zijden de wortel trekken)
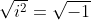
waaruit velen dan concluderen dat
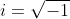
.
Maar dat veronderstelt dat
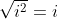
en dat is zoals we bij j zagen een dubieuze bewering.











