Hier een techniek om, als er zijn, gehele nulpunten van een veelterm op te sporen.
Dit werkt alleen als alle coëfficiënten gehele getallen zijn!
Ik begin met de gekende: De getallen die in aanmerking komen zijn delers van de constante term.
VB:
=3x^3-6x^2-4x+8)
. De delers van
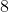
zijn
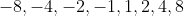
.
Dat zijn de enige mogelijkheden, maar je moet nog steeds controleren ofdat hun functiewaarde wel

is. En als je ze een voor een controleert zou je moeten vinden dat
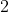
alleen voldoet.
En nu een techniek die ik zelf heb uitgevonden:
Bereken de som van alle coëfficiënten, en noem die

. Bepaal alle delers van

, en tel er steeds
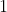
bij op. De bekomen getallen zijn kandidaat-nulpunt.
VB:
=3x^3-6x^2-4x+8)
. De som
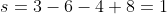
. De delers van
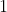
zijn
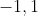
. Tel daar steeds
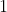
bij op, en we bekomen
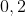
. We moeten deze getallen nog controleren, en inderdaad blijkt
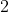
de enige oplossing.
Het lijkt nu alsof die tweede techniek de handigste is, maar dat is ook niet steeds waar. Het beste is als je ze allebei gebruikt. De mogelijke oplossingen moeten dan bij elk van de technieken tevoorschijn komen.
Nu geef ik nog een bewijsje voor die laatste regel, voor wie het niet gelooft:
Laat
)
een functie zijn die de som van de cijfers van een veelterm
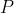
geeft. (Dus eigenlijk is
=P(1))
.)
Je hebt de veelterm
)
, en
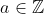
is een nulpunt van
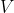
.
Dat betekent dat
)
kan worden geschreven in de vorm
=(x-a)*Q(x))
, waarbij
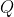
de quotiëntveelterm is.
We hebben dat
=S((x-a)*Q(x))=S(x*Q(x)-a*Q(x))=S(x*Q(x))-a*S(Q)=S(Q)-a*S(Q)=(1-a)*S(Q))
.
Dus
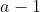
is een deler van
)
.
(Of korter:
=V(1)=(1-a)*Q(1))
.)
Given that, by scientifical reasons, the state of an object is completely determined by the physical influence of its environment, the probability to roll six with a dice is either one or zero.

