Combinaties met dobbelsteen
Combinaties met dobbelsteen
Hallo,
Ik ben momenteel bezig met mijn kennis omtrent statistieken wat bij te schaven.
Hoewel ik al veel onderwerpen heb gevonden hier op het forum die een probleem met "dobbelstenen" behandelen, heb ik het antwoord van mijn vraag nog steeds niet kunnen vinden.
>> Combinaties:
Stel dat je 5 keer met een dobbelsteen gooit, hoeveel mogelijkheden zijn er dan dat het vijftal van dobbelstenen precies drie keer het cijfer 2 bevat.
Ik weet dat er bij 5 dobbelstenen 7776 verschillende mogelijkheden zijn, maar verder zit ik een beetje vast.
Zelf dacht ik dat ik doormiddel van een drietal wel de oplossing zou vinden, maar op die manier slaag ik er echter niet in.
Hopelijk kunnen jullie me helpen.
Ik ben momenteel bezig met mijn kennis omtrent statistieken wat bij te schaven.
Hoewel ik al veel onderwerpen heb gevonden hier op het forum die een probleem met "dobbelstenen" behandelen, heb ik het antwoord van mijn vraag nog steeds niet kunnen vinden.
>> Combinaties:
Stel dat je 5 keer met een dobbelsteen gooit, hoeveel mogelijkheden zijn er dan dat het vijftal van dobbelstenen precies drie keer het cijfer 2 bevat.
Ik weet dat er bij 5 dobbelstenen 7776 verschillende mogelijkheden zijn, maar verder zit ik een beetje vast.
Zelf dacht ik dat ik doormiddel van een drietal wel de oplossing zou vinden, maar op die manier slaag ik er echter niet in.
Hopelijk kunnen jullie me helpen.
Re: Combinaties met dobbelsteen
De volgorde van de individuele uitkomsten is hier belangrijk:
de rij (1,2,3,4,5) is een andere mogelijke uitkomst dan de rij (5,4,3,2,1)
Anders kom je niet tot 6 x 6 x 6 x 6 x 6 = 7776 mogelijke einduitkomsten
We tellen dus rijen, en geen verzamelingen.
We kijken nu eerst naar een rij die begint met drie twee-en:
(2,2,2,a,b):
de eerste 3 worpen leveren een 2, de vierde en vijfde worp een ander getal dan 2: 1, 3, 4, 5 of 6
Hoeveel verschillende van dergelijke rijen bestaan er?
Dan kijken we naar de verdeling van de twee-en:
Op hoeveel manieren kan je de 3 twee-en over de 5 beschikbare plaatsen verdelen.
Wat is tenslotte het antwoord op de vraag?
de rij (1,2,3,4,5) is een andere mogelijke uitkomst dan de rij (5,4,3,2,1)
Anders kom je niet tot 6 x 6 x 6 x 6 x 6 = 7776 mogelijke einduitkomsten
We tellen dus rijen, en geen verzamelingen.
We kijken nu eerst naar een rij die begint met drie twee-en:
(2,2,2,a,b):
de eerste 3 worpen leveren een 2, de vierde en vijfde worp een ander getal dan 2: 1, 3, 4, 5 of 6
Hoeveel verschillende van dergelijke rijen bestaan er?
Dan kijken we naar de verdeling van de twee-en:
Op hoeveel manieren kan je de 3 twee-en over de 5 beschikbare plaatsen verdelen.
Wat is tenslotte het antwoord op de vraag?
Re: Combinaties met dobbelsteen
Beste Arie,
Bedankt voor de snelle reactie. Ik ga het eens opnieuw bekijken.
Het antwoord op de vraag zou 250 moeten zijn.
Bedankt voor de snelle reactie. Ik ga het eens opnieuw bekijken.
Het antwoord op de vraag zou 250 moeten zijn.
Re: Combinaties met dobbelsteen
Dat eindantwoord klopt, maar het was eigenlijk mijn bedoeling dat je dat zou afleiden uit:
- het aantal mogelijke rijtjes waarbij de 3 2en voorop staan, gevolgd door 2 niet-2en,
vermenigvuldigd met
- het aantal mogelijkheden om 3 2en over 5 plaatsen te verdelen.
In de tweede stap tel je dus alle rijtjes
(2,2,2,a,b)
(2,2,a,2,b)
(2,2,a,b,2)
...
(a,b,2,2,2)
waarbij a en b (verschillende of gelijke) niet-2-getallen zijn.
Kom je er met die hints uit?
- het aantal mogelijke rijtjes waarbij de 3 2en voorop staan, gevolgd door 2 niet-2en,
vermenigvuldigd met
- het aantal mogelijkheden om 3 2en over 5 plaatsen te verdelen.
In de tweede stap tel je dus alle rijtjes
(2,2,2,a,b)
(2,2,a,2,b)
(2,2,a,b,2)
...
(a,b,2,2,2)
waarbij a en b (verschillende of gelijke) niet-2-getallen zijn.
Kom je er met die hints uit?
Re: Combinaties met dobbelsteen
Arie,
Ontzettend bedankt.
Ik heb het rustig even uitgetekend op papier en heb het antwoord gevonden.
Er zijn 10 verschillende mogelijkheden om 3x de "2" te plaatsen in een rijtje van 5.
De andere 2 vakjes kunnen dan steeds door 5^2 andere getallen worden gevuld.
(5^2)*10 = 250
Ik denk dat ik vooral de juiste vragen moet leren stellen aan mezelf. Eens ik dat kan zal ik al een stuk verder zijn.
Bedankt voor de hulp man!
edit: Wat ik zelf wel nog niet zie is hoe ik dit eventueel dmv. "permutatie" zou kunnen oplossen, of is dit niet van toepassing hier?
Ontzettend bedankt.
Ik heb het rustig even uitgetekend op papier en heb het antwoord gevonden.
Er zijn 10 verschillende mogelijkheden om 3x de "2" te plaatsen in een rijtje van 5.
De andere 2 vakjes kunnen dan steeds door 5^2 andere getallen worden gevuld.
(5^2)*10 = 250
Ik denk dat ik vooral de juiste vragen moet leren stellen aan mezelf. Eens ik dat kan zal ik al een stuk verder zijn.
Bedankt voor de hulp man!
edit: Wat ik zelf wel nog niet zie is hoe ik dit eventueel dmv. "permutatie" zou kunnen oplossen, of is dit niet van toepassing hier?
Re: Combinaties met dobbelsteen
Welke permutatie bedoel je ...
Re: Combinaties met dobbelsteen
Die voor het samenstellen van een verzameling (zonder herhalingen).SafeX schreef:Welke permutatie bedoel je ...
>> Combinatie van n elementen k aan k genomen?
Of klopt dit niet?
Re: Combinaties met dobbelsteen
Ok, je bedoelt:
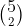
Dit noemen we combinaties (zonder herhaling). Hier het aantal combinaties van 2 uit 5 ...
Dit noemen we combinaties (zonder herhaling). Hier het aantal combinaties van 2 uit 5 ...
Re: Combinaties met dobbelsteen
wat is dan het verschil met permutaties??
http://www.getal-ruimte.nl
Re: Combinaties met dobbelsteen
Een permutatie is een rangschikking, bv hoe kan de letters abc rangschikken elke rangschikking is dan een permutatie ...
Re: Combinaties met dobbelsteen
Duidelijkste uitleg die ik ooit heb gekregen omtrent een permutatie.SafeX schreef:Een permutatie is een rangschikking, bv hoe kan de letters abc rangschikken elke rangschikking is dan een permutatie ...
Helemaal top! Bedankt voor de vlotte hulp!

