Je gedachtegang is prima, voor de overzichtelijkheid kunnen we het ook iets anders opschrijven:
Definieer de volgende kansen:
Code: Selecteer alles
P | Y=c Y=d |
---------------------------
X=a | p q | p+q
X=b | r s | r+s
---------------------------
| p+r q+s | 1
Dan is
E[XY] = pac + qad + rbc + sbd
E[X] = (p+q)a + [1-(p+q)]b
E[Y] = (p+r)c + [1-(p+r)]d
en wordt het product E[X]*E[Y]:
E[X]*E[Y] = [(p+q)a + [1-(p+q)]b] * [(p+r)c + [1-(p+r)]d]
= (p+q)(p+r)ac + (p+q)[1-(p+r)]ad + [1-(p+q)](p+r)bc + [1-(p+q)][1-(p+r)]bd
= (p+q)(p+r)ac + [p+q - (p+q)(p+r)]ad + [p+r - (p+q)(p+r)]bc + [1-(p+q)-(p+r) + (p+q)(p+r)]bd
(werk nu de laatste term iets verder uit:)
= (p+q)(p+r)ac + [p+q - (p+q)(p+r)]ad + [p+r - (p+q)(p+r)]bc + [(1-p-q-r) - p + (p+q)(p+r)]bd
= (p+q)(p+r)ac + [p+q - (p+q)(p+r)]ad + [p+r - (p+q)(p+r)]bc + [s - p + (p+q)(p+r)]bd
en gegeven is dat dit geheel gelijk is aan E[XY]:
= pac + qad + rbc + sbd
Dit is wat jij ook had.
Breng nu alles naar 1 kant:
[-p+(p+q)(p+r)]ac + [p - (p+q)(p+r)]ad + [p - (p+q)(p+r)]bc + [- p + (p+q)(p+r)]bd = 0
definieer: k = [p-(p+q)(p+r)], dan kunnen we ook schrijven:
-kac + kad + kbc - kbd = 0
Stel k is ongelijk aan nul, dan kunnen we door k delen:
-ac + ad + bc - bd = 0
a(d-c) -b(d-c) = 0
(a-b)*(d-c) = 0
dan is a=b en/of d=c, maar gegeven was dat a en b precies 2 waardes aannemen, dus a ongelijk b.
Ook was gegeven dat c en d verschillend zijn, dus moet k gelijk aan nul zijn:
k = 0
[p-(p+q)(p+r)] = 0
p = (p+q)(p+r)
ofwel
P(X=a, Y=c) = P(X=a) * P(Y=c).
Evenzo voor de andere kansen.
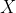 en
en 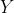 zijn twee discrete stochasten, die ieder precies 2 waardes aannemen, met de eigenschap dat
zijn twee discrete stochasten, die ieder precies 2 waardes aannemen, met de eigenschap dat =\mathbb{E}(X)\mathbb{E}(Y)) .
.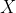 en
en 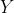 onafhankelijk zijn.
onafhankelijk zijn.+ad\mathbb{P}(X=a,Y=d)+bc\mathbb{P}(X=b,Y=c)+bd\mathbb{P}(X=b,Y=d) = ac\mathbb{P}(X=a)\mathbb{P}(Y=c)+ad\mathbb{P}(X=a)\mathbb{P}(Y=d)+bc\mathbb{P}(X=b)\mathbb{P}(Y=c)+bd\mathbb{P}(X=b)\mathbb{P}(Y=d))
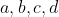 vaste constantes zijn, kan ik hieruit niet direct concluderen dat
vaste constantes zijn, kan ik hieruit niet direct concluderen dat =\mathbb{P}(X=a)\mathbb{P}(Y=c)) , etc. zoals gewenst zou zijn.
, etc. zoals gewenst zou zijn.