berekening relatieve fout
berekening relatieve fout
@arie Je gaat er vanuit dat de absolute fout op F1 en F2 dezelfde is. Ik denk dat dat niet de bedoeling is. Alleen de spreiding op deze absolute fout is dezelfde.
Re: berekening relatieve fout
Nee, in mijn formules hierboven is de relatieve fout hetzelfde, namelijk delta = 5% = 0.05 (zoals in de opgave gegeven).wnvl schreef:@arie Je gaat er vanuit dat de absolute fout op F1 en F2 dezelfde is. Ik denk dat dat niet de bedoeling is. Alleen de spreiding op deze absolute fout is dezelfde.
Dus voor alle F_i geldt:
dus:
maar
Re: berekening relatieve fout
Mijn commentaar was fout geformuleerd. Ik bedoelde eigenlijk.
@arie Je gaat er vanuit dat de relatieve fout op F1 en F2 dezelfde is. Ik denk dat dat niet de bedoeling is. Alleen de spreiding op deze relatieve fout is dezelfde.
Ter verduidelijking:
Het kan bvb zijn dat
exacte waarde F1=F1gemeten *(1.03) en
exacte waarde F2=F2gemeten*(0.96)
Jij gaat er van uit dat de exacte relatieve fout bij een concrete meting altijd dezelfde is bij beide krachten
exacte waarde F1=F1gemeten *(1.03) en
exacte waarde F2=F2gemeten*(1.03)
beide relatieve fouten kunnen echter verschillen, maar de spreiding bij verschillende metingen van de fouten moet dezelfde zijn.
@arie Je gaat er vanuit dat de relatieve fout op F1 en F2 dezelfde is. Ik denk dat dat niet de bedoeling is. Alleen de spreiding op deze relatieve fout is dezelfde.
Ter verduidelijking:
Het kan bvb zijn dat
exacte waarde F1=F1gemeten *(1.03) en
exacte waarde F2=F2gemeten*(0.96)
Jij gaat er van uit dat de exacte relatieve fout bij een concrete meting altijd dezelfde is bij beide krachten
exacte waarde F1=F1gemeten *(1.03) en
exacte waarde F2=F2gemeten*(1.03)
beide relatieve fouten kunnen echter verschillen, maar de spreiding bij verschillende metingen van de fouten moet dezelfde zijn.
Re: berekening relatieve fout
Klopt.wnvl schreef:Het kan bvb zijn dat
exacte waarde F1=F1gemeten *(1.03) en
exacte waarde F2=F2gemeten*(0.96)
Klopt niet: de delta hierboven is de maximale relatieve afwijking.wnvl schreef: Jij gaat er van uit dat de exacte relatieve fout bij een concrete meting altijd dezelfde is bij beide krachten
exacte waarde F1=F1gemeten *(1.03) en
exacte waarde F2=F2gemeten*(1.03)
beide relatieve fouten kunnen echter verschillen, maar de spreiding bij verschillende metingen van de fouten moet dezelfde zijn.
Zie ook de vraagstelling van Christa1901: ..."De beide krachten zijn gemeten met een mogelijke fout van 5% ..."
De gemeten waarde kan ook minder dan een factor delta (= 0.05) van de werkelijke waarde af liggen.
Het lijkt me dat (1 +/- delta) de relatieve spreiding is die jij bedoelt.
Re: berekening relatieve fout
Mmm, ik denk dat er mogelijks nog een misverstand is.
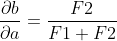
^2})
-aF2}{(F1+F2)^2}=\frac{aF1}{(F1+F2)^2})
Met jou interpretatie van de fout als maximale fout kom ik dan op
^2}0.05F1\vert + \vert\frac{aF1}{(F1+F2)^2}0.05F2\vert)
Is dat dan ook jou oplossing?
Voor alle duidelijkheid, ik kom opwnvl schreef:eerste vraag:
Eerste stap is het berekenen van de partiële afgeleiden naar a, F1 en F2.
Met jou interpretatie van de fout als maximale fout kom ik dan op
Is dat dan ook jou oplossing?
Re: berekening relatieve fout
Nee, voor de totale relatieve fout gebruik ik:
 \cdot (1 \pm \delta)}{(1 \pm \delta)} \approx 1 \pm (\epsilon + 2 \delta))
in dit geval dus: 1 +/- 0.12
en omdat aF2/(F1+F2) = 3 wordt de absolute fout 0.36.
PS:
onderwerp gesplitst: deze discussie gaat beduidend dieper dan vraag in oorspronkelijke topic:
viewtopic.php?f=23&t=9421
in dit geval dus: 1 +/- 0.12
en omdat aF2/(F1+F2) = 3 wordt de absolute fout 0.36.
PS:
onderwerp gesplitst: deze discussie gaat beduidend dieper dan vraag in oorspronkelijke topic:
viewtopic.php?f=23&t=9421
Re: berekening relatieve fout
Ik denk dat je vergeet dat teller en noemer in dit geval niet onafhankelijk zijn. In beiden komt F2 voor.
Stel bvb dat F2=10000000 en F1=1
In dat geval gaat gelden dat b=a (F1 is te verwaarlozen en F2 deel je weg in teller en noemer) en de relatieve fout zal zijn. Jou formule gaat nog altijd als relatieve fout
zijn. Jou formule gaat nog altijd als relatieve fout 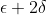 . Merk op dat mijn formule met de partieel afgeleiden, wel een juist antwoord zou geven.
. Merk op dat mijn formule met de partieel afgeleiden, wel een juist antwoord zou geven.
Als de formule voor b was
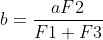
,dan was het een ander verhaal.
Stel bvb dat F2=10000000 en F1=1
In dat geval gaat gelden dat b=a (F1 is te verwaarlozen en F2 deel je weg in teller en noemer) en de relatieve fout zal
Als de formule voor b was
,dan was het een ander verhaal.
Re: berekening relatieve fout
Je hebt gelijk.
Ik had niet gelet op die afhankelijkheid.
Jouw formule is dus de correcte:
^2}0.05F_1\right|)
)
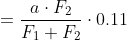
waarmee het antwoord 0.33 wordt.
De cursus van Christa1901 gaat echter niet zo ver: die houden het op 0.36 als antwoord...
Ik had niet gelet op die afhankelijkheid.
Jouw formule is dus de correcte:
waarmee het antwoord 0.33 wordt.
De cursus van Christa1901 gaat echter niet zo ver: die houden het op 0.36 als antwoord...


