Ik heb een vraag over hoe ik het gedrag van een exponent tussen de 0 en 1 moet begrijpen. Gegeven was een serie getallen met een exponentieel verband en een groeifactor 1,41^{t}. Nu stond in de desbetreffende opgave het exponent voor de tijd waarbij 1=30 jaar. Nu moest er een waarde worden berekend waarbij 20 jaar wordt geteld. Nu begrijp ik hoe ik aan mijn antwoord moet komen: 1,41^{(1*2/3)} Dus eigenlijk 1,41^{0,67}.
Nu had ik het antwoord wel juist, maar ik kwam er achter dat ik eigenlijk niet begrijp wat er nu precies gebeurd. Ik dacht: 1,41*(1,41*0,67) = 1,41*0,9447. Dit blijkt echter niet te kloppen als ik mijn antwoord bereken via deze route. Kan iemand mij misschien uitleggen hoe ik een dergelijke som moet opvatten? Ik begrijp dat bijvoorbeeld: 5+1,2^{3} te schrijven is als: (5+1,2*1,2*1,2). Maar bij een negatief exponent kom ik er dus niet uit.
Vraag over groeifactor met exponent 0<e<1
Re: Vraag over groeifactor met exponent 0<e<1
Ik zie geen nu negatieve exponent ...
2^(2/3) is per definitie (daarmee kan je breuken in de exponent toelaten):
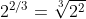
Kun je dit schatten ...
2^(2/3) is per definitie (daarmee kan je breuken in de exponent toelaten):
Kun je dit schatten ...
Re: Vraag over groeifactor met exponent 0<e<1
Ik zie dat ik op het laatst negatieve exponent zei, dat bedoelde ik niet. Ik heb het hier over een exponent tussen de 0 en 1. U zegt: “2^(2/3) is per definitie”. Wat bedoelt u hiermee? Dat laatste wat u geeft kan ik niet schatten want ik begrijp niet wat er gebeurt wanneer een exponent tussen 0 en 1 ligt. Is er niet een equivalent wat u mij kan geven van 2^(3) = 2*2*2? Is bijvoorbeeld 2^(3/4) zo te schrijven?SafeX schreef:Ik zie geen nu negatieve exponent ...
2^(2/3) is per definitie (daarmee kan je breuken in de exponent toelaten):
Kun je dit schatten ...
Re: Vraag over groeifactor met exponent 0<e<1
kijk naar de definitie!
Je kan ook het volgende bedenken 2^(2/3) ligt (op de getallenlijn) tussen 2^0 en 2^1 (vind je dat logisch?)
Wat weet je van (bv) 2^(1/2)?
Je kan ook het volgende bedenken 2^(2/3) ligt (op de getallenlijn) tussen 2^0 en 2^1 (vind je dat logisch?)
Wat weet je van (bv) 2^(1/2)?
Re: Vraag over groeifactor met exponent 0<e<1
Stel dat je linker- en rechterlid tot de 3e macht verheft, wat krijg je dan ...SafeX schreef:
Re: Vraag over groeifactor met exponent 0<e<1
Dat klinkt mij in principe logisch als ik me een getallenlijn voorstel met 2^0, 2^1, 2^2 etc. Dan stel ik me voor dat het getal tussen 2^0 en 2^1 ergens tussen de 1 en 2 ligt. Betekent dit dat ik naar dit soort getallen tussen 0 en 1 moet kijken als waarden op zichzelf op de getallenlijn van X^0 t/m X^1? Als dit zo is verheldert dit de zaak wel. Ik snap echter nog niet waaromSafeX schreef:kijk naar de definitie!
Je kan ook het volgende bedenken 2^(2/3) ligt (op de getallenlijn) tussen 2^0 en 2^1 (vind je dat logisch?)
Wat weet je van (bv) 2^(1/2)?
-
arno
- Vergevorderde
- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Vraag over groeifactor met exponent 0<e<1
StelJacko1996 schreef:Ik snap echter nog niet waarom
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Vraag over groeifactor met exponent 0<e<1
Dat laatste is een definitie en wat je moet begrijpen is dat deze definitie op logische wijze breuken in de exponent toelaat ...Jacko1996 schreef:bijvoorbeeldheb, dat dit ook
is. Maar begrijp niet waarom.
Laten we even kijken naar je vb.
Merk op de exponenten zijn positief gehele getallen
De oplossing van deze verg is:
Ook dit is een afspraak (definitie) en dat is niet anders als de generalisering van de vierkantswortel
x is dus een getal zodanig dat x^9= x*x*...*x het getal 4^8 oplevert ...
Kan je het dichtstbijzijnde gehele getal zonder RM vinden en met RM ook de eerste decimaal ...
Maar dan kan x ook geschreven worden als 4^(8/9), immers:
Welke rekenregel voor exponenten heb ik nu toegepast?
Re: Vraag over groeifactor met exponent 0<e<1
Ik snap wat Arno vertelt, en kan de serie volgen, en snap daarom ook waaromSafeX schreef:Dat laatste is een definitie en wat je moet begrijpen is dat deze definitie op logische wijze breuken in de exponent toelaat ...Jacko1996 schreef:bijvoorbeeld
Laten we even kijken naar je vb.
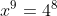
Merk op de exponenten zijn positief gehele getallen
De oplossing van deze verg is:
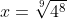
Ook dit is een afspraak (definitie) en dat is niet anders als de generalisering van de vierkantswortel
x is dus een getal zodanig dat x^9= x*x*...*x het getal 4^8 oplevert ...
Kan je het dichtstbijzijnde gehele getal zonder RM vinden en met RM ook de eerste decimaal ...
Maar dan kan x ook geschreven worden als 4^(8/9), immers:
Welke rekenregel voor exponenten heb ik nu toegepast?
Re: Vraag over groeifactor met exponent 0<e<1
Ik loop overigens tegen een vergelijkbaar soort ongemak aan met onbekende exponenten vinden via logaritmen. Ik kan alle antwoorden vinden met de GR zonder moeite, maar heb wederom geen idee wat er werkelijk gebeurt. Hierdoor voelt wiskunde als een soort truc. Ik heb het dan over vraagstukken in de vorm van: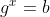 
waarbij x onbekend is. Via de functie }{log(g)})
vind ik de antwoorden van x,en ik begrijp dus dat dit is wat het doet, maar ik weet niet waarom. Als mijn vorige antwoord nog niet juist was wil ik graag eerst inzicht in die vraag, maar dit wellicht voor later...
Re: Vraag over groeifactor met exponent 0<e<1
Precies, maar 8/9*9= ... je kan gelijk vereenvoudigen immers je hebt eenzelfde factor 9 in teller en noemer. Dus eerst 8*9 en daarna delen door 9 is een omweg ...Jacko1996 schreef:Ik snap in principe datwant
Is dit wat u bedoelt met de rekenregel?
Zoek eens (op internet) naar rekenregels voor machten en exponenten ...
De notatie a^p betekent p factoren a. Kennismaken met zo'n notatie houdt in dat je je vertrouwd moet maken met de rekenregels die daaruit volgen ...
Eén daarvan is: (a^p)^q=a^(pq), maar dat geldt voor p en q positief geheel
Kijk dan als vb naar
Wat voor exponent moet hier nu staan ... ? Tot nu toe hebben we alleen pos gehele getallen.
Nu moet je natuurlijk eerst weten wat de definitie van de wortel is, ga dat na ...
Waarom worden machten en logaritmen in één adem genoemd, natuurlijk omdat een logaritme een exponent is van een grondtal, ga dat na en vanzelfsprekend volgt weer (net zoals eerder bij machten) dat je je vertrouwd moet maken met deze (nieuwe) notatie via de daarbij behorende rekenregels ...
Re: Vraag over groeifactor met exponent 0<e<1
SafeX schreef:Precies, maar 8/9*9= ... je kan gelijk vereenvoudigen immers je hebt eenzelfde factor 9 in teller en noemer. Dus eerst 8*9 en daarna delen door 9 is een omweg ...Jacko1996 schreef:Ik snap in principe dat
Zoek eens (op internet) naar rekenregels voor machten en exponenten ...
De notatie a^p betekent p factoren a. Kennismaken met zo'n notatie houdt in dat je je vertrouwd moet maken met de rekenregels die daaruit volgen ...
Eén daarvan is: (a^p)^q=a^(pq), maar dat geldt voor p en q positief geheel
Kijk dan als vb naar
Wat voor exponent moet hier nu staan ... ? Tot nu toe hebben we alleen pos gehele getallen.
Nu moet je natuurlijk eerst weten wat de definitie van de wortel is, ga dat na ...
Waarom worden machten en logaritmen in één adem genoemd, natuurlijk omdat een logaritme een exponent is van een grondtal, ga dat na en vanzelfsprekend volgt weer (net zoals eerder bij machten) dat je je vertrouwd moet maken met deze (nieuwe) notatie via de daarbij behorende rekenregels ...
Ik begrijp de vereenvoudiging en voer deze normaliter zelf ook uit. Omdat u vroeg om de rekenregel dacht ik het nodig om even de “omweg” te nemen en de breuken te vermenigvuldigen om inzicht te tonen. Ook de notatie a^p en het werken met deze in functies snap ik denk ik wel. Uw gegeven: (a^p)^q=a^(pq) begrijp ik dan ook goed. Betreffende uw voorbeeld:
Ik kom hier als volgt aan:
Met in mijn achterhoofd de reeds opgedane kennis over definities van de wortel gegeven door Arno beredeneer ik:
0) Gegeven is vraagstuk:
1)
2)
3) Via mijn kennis van exponenten vermenigvuldigen begrijp ik dat het 0,5*2 moet zijn.
4)Ergo:
Als dit in orde is wil ik daarna verder gaan over logaritmen. Omdat als ik hier nog fouten bega en de twee gecorreleerd zijn, het mogelijk verspilde tijd is om er nu vragen over te stellen.
Re: Vraag over groeifactor met exponent 0<e<1
Ok, het is nu dus duidelijk dat op basis van die RR (rekenregel), we nu kunnen afspreken dat de exponent van een macht ook een breuk kan zijn.
De definitie luidt dus:
})
met p en q geheel
Op basis van welke RR kunnen we negatieve exponenten toelaten?
Tenslotte: je hebt nu kunnen zien:
1. er is nieuwe notatie: de macht
2. daaruit volgen rekenregels (RR) voor machten
3. die RR (op hun beurt) zijn bruikbaar om de toegelaten getallen weer uit te breiden
De definitie luidt dus:
Op basis van welke RR kunnen we negatieve exponenten toelaten?
Tenslotte: je hebt nu kunnen zien:
1. er is nieuwe notatie: de macht
2. daaruit volgen rekenregels (RR) voor machten
3. die RR (op hun beurt) zijn bruikbaar om de toegelaten getallen weer uit te breiden
Re: Vraag over groeifactor met exponent 0<e<1
Over de RR die ons in staat stellen negatieve exponenten toe te laten ben ik niet zeker, omdat mijn intuïtie zegt dat dit hetzelfde is als ik al liet zien, maar volgens mij bedoelt u dit niet? Ik zou zeggen dat dit aantoont dat negatieve exponenten zijn toegestaan:SafeX schreef:Ok, het is nu dus duidelijk dat op basis van die RR (rekenregel), we nu kunnen afspreken dat de exponent van een macht ook een breuk kan zijn.
De definitie luidt dus:
Op basis van welke RR kunnen we negatieve exponenten toelaten?
Tenslotte: je hebt nu kunnen zien:
1. er is nieuwe notatie: de macht
2. daaruit volgen rekenregels (RR) voor machten
3. die RR (op hun beurt) zijn bruikbaar om de toegelaten getallen weer uit te breiden
Re: Vraag over groeifactor met exponent 0<e<1
Dit kan niet, de wortelexponent (bij jou -2) mag niet negatief zijn.Jacko1996 schreef:
})
^{-2}= 16^{1})
}\right )^{-2}=16^{1})
Dit klopt niet! Wat is: 3^3*3^4= ...
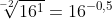
Kijk eens naar:Over de RR die ons in staat stellen negatieve exponenten toe te laten ben ik niet zeker, omdat mijn intuïtie zegt dat dit hetzelfde is als ik al liet zien, maar volgens mij bedoelt u dit niet? Ik zou zeggen dat dit aantoont dat negatieve exponenten zijn toegestaan:
Kies dan p=0 (mag dat?)