Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Dit forum is voor het voortgezetonderwijs (of 2de/3de graad ASO), als je in de bovenbouw zit. We gaan er vanuit dat je een Grafische Rekenmachine hebt.
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 15 mar 2017, 15:20
Hallo,
Ik wil onderstaande functie ontbinden en factoren:
= x^3-3x^2-9x-5=0)
?
Maar hoe pak ik dit aan met 4-termen ? De gemeenschappelijke factor eruit halen wil niet en ook in twee splitsen wil niet.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 15 mar 2017, 17:18
In principe zoek je een oplossing met gehele getallen, stel x=a. Als dat lukt kan je verdergaan door de ontbinding toe te passen dwz f(x)=(x-a)(...)
Als het niet lukt heb je pech gehad. Teken iig een grafiek!
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 15 mar 2017, 17:32
Je kan f(x) = x^3 - 3x^2 - 9x + 5 ontbinden en f(x) = x^3 - 3x^2 - 9x + 5 = 0 oplossen.
Met behulp van het
rational root theorem kan je zeggen dat er vier mogelijke gehele oplossingen zijn.
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 15 mar 2017, 19:39
SafeX schreef:In principe zoek je een oplossing met gehele getallen, stel x=a. Als dat lukt kan je verdergaan door de ontbinding toe te passen dwz f(x)=(x-a)(...)
Als het niet lukt heb je pech gehad. Teken iig een grafiek!
Oké als ik het goed begrijp uit je reactie is dat niet mogelijk bij deze vergelijking ? Het lukt mij in ieder geval niet..
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 15 mar 2017, 19:41
David schreef:Je kan f(x) = x^3 - 3x^2 - 9x + 5 ontbinden en f(x) = x^3 - 3x^2 - 9x + 5 = 0 oplossen.
Met behulp van het
rational root theorem kan je zeggen dat er vier mogelijke gehele oplossingen zijn.
De rational root therm is helemaal nieuw voor mij. Ik heb het stuk gelezen op Wikipedia , maar het is me nog niet helemaal duidelijk hoe ik dit toe pas op de vergelijking
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 15 mar 2017, 19:55
Voor de vergelijking
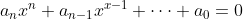
met hele coëfficiënten en
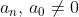
heeft, als de polynoom rationale oplossingen heeft, een oplossing de vorm
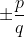
met ggd(p, q) = 1 en
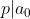
en
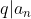
Nu,
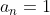
dus q = 1, en
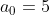
dus p = 1 of 5. Welke waarden kan
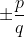
dan hebben?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 15 mar 2017, 20:32
Ga na dat f(x) = 0 als x = 5. Dit betekent dat x-5 een factor is van x³-3x²-9x-5. Zie je nu kans om de andere factoren te vinden? Wat worden dus de oplossingen van f(x) = 0?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 15 mar 2017, 22:10
Westerwolde schreef:Het lukt mij in ieder geval niet..
Heb je x=-1 al geprobeerd?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 16 mar 2017, 10:29
Overigens de gegeven functie is :
=\frac{(x-1)^2(x+5)}{4})
Deze had ik zelf al verder uitgewerkt naar :
= x^3+3x^2-9x+5=0)
Had ik misschien in de eerste stap al iets anders kunnen doen zodat we 'beter' uit zouden komen ?
-
David
- Moderator

- Berichten: 4927
- Lid geworden op: 14 mei 2009, 16:22
Bericht
door David » 16 mar 2017, 13:01
De twee functies die je geeft hebben vereenvoudigd verschillende waarden voor de coëfficiënt van x^3. Wat is je eerste stap?
Stap 1 van het oplossen van een probleem is te erkennen dat je een probleem hebt.
(Raffiek Torreman)
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 16 mar 2017, 13:14
David schreef:De twee functies die je geeft hebben vereenvoudigd verschillende waarden voor de coëfficiënt van x^3. Wat is je eerste stap?
= (x-1)^2)
=
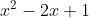
=>
)
=
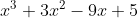
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 16 mar 2017, 16:53
Westerwolde schreef:Overigens de gegeven functie is :
=\frac{(x-1)^2(x+5)}{4})
Deze had ik zelf al verder uitgewerkt naar :
= x^3+3x^2-9x+5=0)
Dat klopt niet behalve voor x=1 en x=-5
Wat betekent =0 bij de tweede functie, want dan heb je geen functie meer maar een verg.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 16 mar 2017, 19:14
Westerwolde schreef:Hallo,
Ik wil onderstaande functie ontbinden en factoren:
= x^3-3x^2-9x-5=0)
?
Je kende de ontbinding dus, waarom vraag je daar dan naar?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 16 mar 2017, 19:38
SafeX schreef:Westerwolde schreef:Hallo,
Ik wil onderstaande functie ontbinden en factoren:
= x^3-3x^2-9x-5=0)
?
Je kende de ontbinding dus, waarom vraag je daar dan naar?
Ik moet de snijpunten met de x-as vinden, dan moet ik de vergelijking toch herleiden op nul ?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 16 mar 2017, 19:48
Geef eens even de letterlijke tekst van de opgave.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel






?

?
