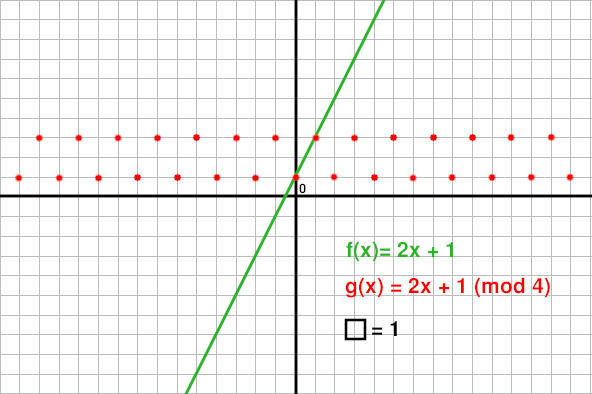
Grafische weergave van g(x) = 2x + 1 (mod 4)
-
Harald1970
- Nieuw lid

- Berichten: 2
- Lid geworden op: 13 jun 2020, 15:17
Grafische weergave van g(x) = 2x + 1 (mod 4)
Is deze grafische weergave van g(x) = 2x + 1 (mod 4) juist?


Re: Grafische weergave van g(x) = 2x + 1 (mod 4)
Als x geheeltallig is \((x \in \mathbb{Z})\) dan klopt dit.
Dit is dan ook het meest gebruikelijke antwoord,
maar dan verwacht je dat dit ook voor f(x) geldt.
Kijk daarom nog eens goed naar de definities in je boek:
- als alleen vereist is dat 2x+1 geheeltallig is, dan zijn er meer oplossingen,
- soms is mod zelfs gedefinieerd over alle reele getallen in \(\mathbb{R}\), bijvoorbeeld
\(3.14 = 1.14\; (\text{mod} \;2)\) en dan wordt de grafiek van g(x) nog anders.
Mogelijk is dit laatste hier het geval.
Dit is dan ook het meest gebruikelijke antwoord,
maar dan verwacht je dat dit ook voor f(x) geldt.
Kijk daarom nog eens goed naar de definities in je boek:
- als alleen vereist is dat 2x+1 geheeltallig is, dan zijn er meer oplossingen,
- soms is mod zelfs gedefinieerd over alle reele getallen in \(\mathbb{R}\), bijvoorbeeld
\(3.14 = 1.14\; (\text{mod} \;2)\) en dan wordt de grafiek van g(x) nog anders.
Mogelijk is dit laatste hier het geval.
-
Harald1970
- Nieuw lid

- Berichten: 2
- Lid geworden op: 13 jun 2020, 15:17
Re: Grafische weergave van g(x) = 2x + 1 (mod 4)
Beste Arie,
Bedankt voor het nakijken! Deze opgave had ik zelf bedacht.
Hier de drie verschillende uitwerkingen waar je het over had. Ik hoop dat ik het goed heb gedaan!
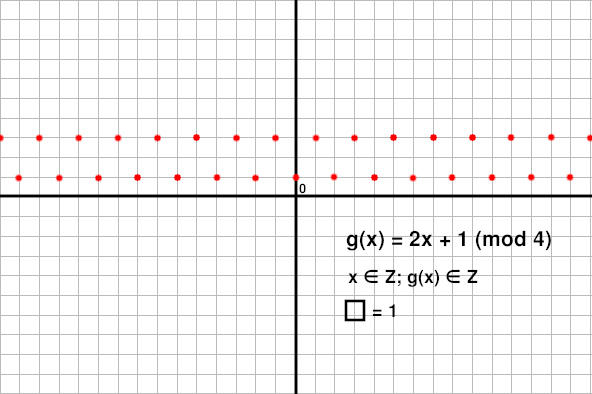
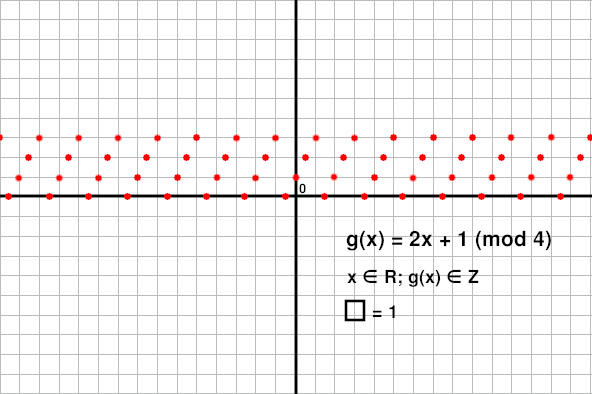
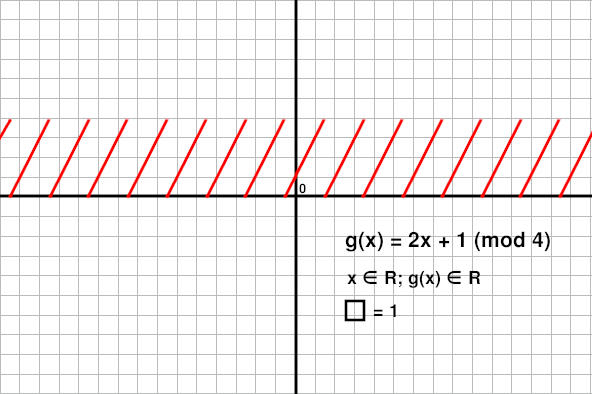
De variant die je noemde van dat mod soms zelfs gedefinieerd wordt over ALLE reële getallen, dat is de 3de toch?
Bedankt voor het nakijken! Deze opgave had ik zelf bedacht.
Hier de drie verschillende uitwerkingen waar je het over had. Ik hoop dat ik het goed heb gedaan!



De variant die je noemde van dat mod soms zelfs gedefinieerd wordt over ALLE reële getallen, dat is de 3de toch?
Re: Grafische weergave van g(x) = 2x + 1 (mod 4)
Het ziet er prima uit.
Leuk bedacht, goed denkwerk!
In de wiskunde is de eerste vorm het meest gebruikelijk:
x (mod m) als functie voor gehele getallen: \(\text{(mod m):} \;\mathbb{Z} \rightarrow \{0, 1, ..., m-1\} \)
In dat geval zou ik de functie f(x) uit je eerste post ook geheeltallig weergeven:

Heb je voor \(x \in \mathbb{Z}\) ook al gekeken hoe de functies
\(g_1(x) = x + 1 \;(\text{mod}\; 4)\)
\(g_3(x) = 3x + 1 \;(\text{mod}\; 4)\)
\(g_4(x) = 4x + 1 \;(\text{mod}\; 4)\)
en
\(g_{-1}(x) = -x + 1 \;(\text{mod}\; 4)\)
er uit zien (bijvoorbeeld voor x=0 t/m x=7)?
- hoe verklaar je wat er aan de hand is in \(g_4(x)\)?
- wat zie je als je \(g_3(x)\) vergelijkt met \(g_{-1}(x)\)?
PS:
Nog een detail: als je mod op \(\mathbb{R}\) definieert:
We geven doorgaans nog aan of de uiteinden van elke flank wel of niet onderdeel zijn van de functie:
- gesloten rondje: het punt op dit uiteinde behoort WEL tot de grafiek van de functie
- open rondje: het punt op dit uiteinde behoort NIET tot de grafiek van de functie
Je krijgt dan zo'n plaatje:

Dan wordt het uit de grafiek direct duidelijk dat bijvoorbeeld het punt (1.5, 0) wel op de grafiek ligt en
het punt (1.5, 4) niet.
PPS:
De middelste variant, waarbij
\(\text{(mod m):} \;\{ ..., -1, -\frac{1}{2}, 0, \frac{1}{2}, 1, \frac{3}{2}, ...\} \rightarrow \{0, 1, ..., m-1\} \)
zal je minder vaak tegenkomen.
In praktijk breiden we het domein dan liever uit naar de hele \(\mathbb{R}\) en krijgen we een periodieke trapfunctie.
Deze wordt doorgaans met behulp van de floor functie gedefinieerd,
zie bv https://en.wikipedia.org/wiki/Floor_and ... _functions.

Leuk bedacht, goed denkwerk!
In de wiskunde is de eerste vorm het meest gebruikelijk:
x (mod m) als functie voor gehele getallen: \(\text{(mod m):} \;\mathbb{Z} \rightarrow \{0, 1, ..., m-1\} \)
In dat geval zou ik de functie f(x) uit je eerste post ook geheeltallig weergeven:

Heb je voor \(x \in \mathbb{Z}\) ook al gekeken hoe de functies
\(g_1(x) = x + 1 \;(\text{mod}\; 4)\)
\(g_3(x) = 3x + 1 \;(\text{mod}\; 4)\)
\(g_4(x) = 4x + 1 \;(\text{mod}\; 4)\)
en
\(g_{-1}(x) = -x + 1 \;(\text{mod}\; 4)\)
er uit zien (bijvoorbeeld voor x=0 t/m x=7)?
- hoe verklaar je wat er aan de hand is in \(g_4(x)\)?
- wat zie je als je \(g_3(x)\) vergelijkt met \(g_{-1}(x)\)?
PS:
Nog een detail: als je mod op \(\mathbb{R}\) definieert:
We geven doorgaans nog aan of de uiteinden van elke flank wel of niet onderdeel zijn van de functie:
- gesloten rondje: het punt op dit uiteinde behoort WEL tot de grafiek van de functie
- open rondje: het punt op dit uiteinde behoort NIET tot de grafiek van de functie
Je krijgt dan zo'n plaatje:

Dan wordt het uit de grafiek direct duidelijk dat bijvoorbeeld het punt (1.5, 0) wel op de grafiek ligt en
het punt (1.5, 4) niet.
PPS:
De middelste variant, waarbij
\(\text{(mod m):} \;\{ ..., -1, -\frac{1}{2}, 0, \frac{1}{2}, 1, \frac{3}{2}, ...\} \rightarrow \{0, 1, ..., m-1\} \)
zal je minder vaak tegenkomen.
In praktijk breiden we het domein dan liever uit naar de hele \(\mathbb{R}\) en krijgen we een periodieke trapfunctie.
Deze wordt doorgaans met behulp van de floor functie gedefinieerd,
zie bv https://en.wikipedia.org/wiki/Floor_and ... _functions.

