Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Dit forum is voor het voortgezetonderwijs (of 2de/3de graad ASO), als je in de bovenbouw zit. We gaan er vanuit dat je een Grafische Rekenmachine hebt.
-
Peter1965
- Nieuw lid

- Berichten: 1
- Lid geworden op: 14 nov 2012, 13:36
Bericht
door Peter1965 » 14 nov 2012, 13:43
Hieronder zien jullie een piramide met een regelmatig 8 hoekig grondvlak;
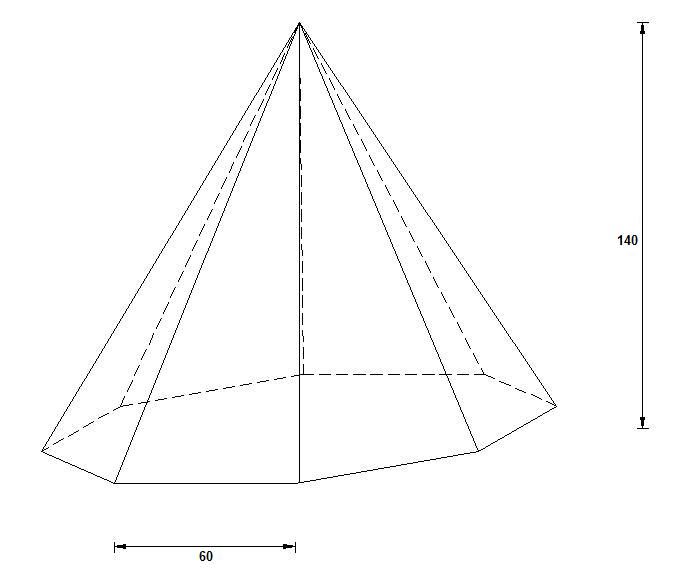
Grondvlak piramide:
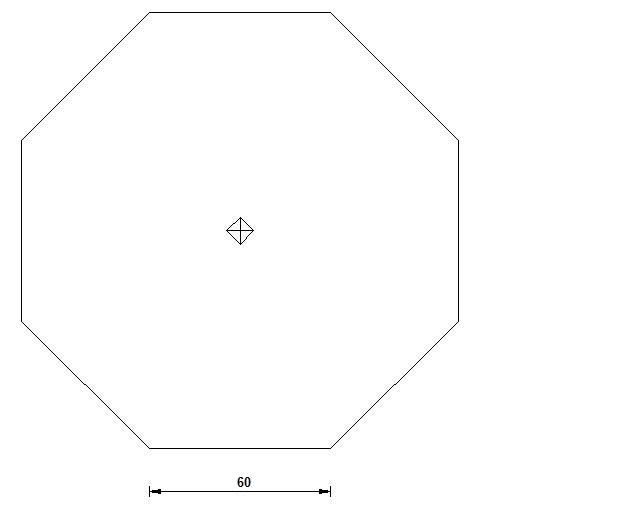
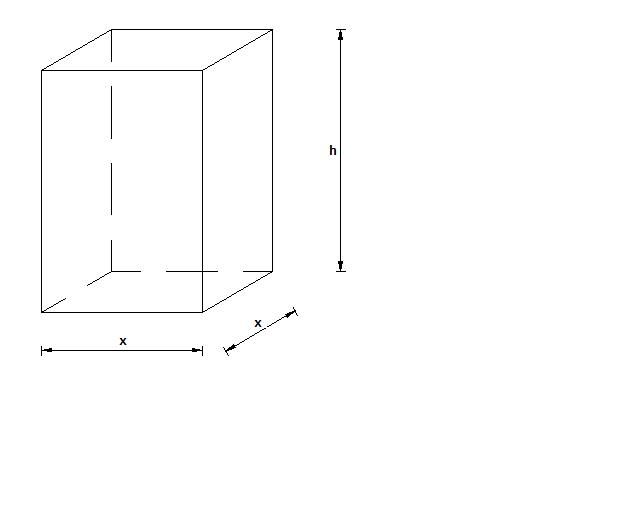
In de piramide kunnen allerlei vormen worden geplaatst. Zo ook onderstaande balk met grondvlak x2 en hoogte h. De balk kan voor verschillende waarden x en h in de piramide worden geplaatst.
De opgave is als volgt: zoek uit bij welke waarden van x en h de balk een maximale inhoud heeft in de piramide en bereken deze maximale inhoud.
Laat ook zien hoe je tot je berekening bent gekomen!
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 14 nov 2012, 14:54
Ik zie in het grondvlak al hoe je vierkant komt te liggen?
Z0 ja, is dat je eigen idee of is dit gegeven?
Neem dit dan nu aan. Hoe kan je dan hoogte h bepalen?
-
jogo
- Vast lid

- Berichten: 52
- Lid geworden op: 25 apr 2007, 17:09
- Locatie: genk
Bericht
door jogo » 17 mar 2013, 11:54
Mooie opgave.
Het grootst denkbare vierkant dat nog in een regelmatige achthoek gaat , is een vierkant dat met zijn 4 hoekpunten samenvalt met vier van de 8 hoekpunten (en ribben) van de piramide (hoekpunt 2,4,6,8).
De hoogte van de balk met dit vierkantig grondvak dat nog in de piramide kan is echter nul (volume nul).Verkleinen we stapsgewijs het vierkantig grondvak (zonder de oriëntatie te wijzigen,hoekpunten bovenvlak balk rakend aan 4 ribben van de piramide, dan vergroot stelselmatig de hoogte van de mogelijke inwendige balk, tot een maximale hoogte, de hoogte van de piramide, en een grondvlak nul bereikt is (volume nul).
Het verloop van het volume van de denkbaar inwendige balken gaat dus beginnend met nul (grootste grondvlak maal hoogte nul ) toenemend tot ergens een maximaal volume om dan weer te verminderen naar nul ,maximale hoogte =hoogte piramide, maal nul grondvlak (top piramide)
Om de balk met het maximaal volume te vinden moeten we dat in eerst een functie schrijven en dan de differentiaal zoeken denk ik, maar dat zal ik zonder hulp niet kunnen.
Ik zal zien hoe ver ik geraak.
-
jogo
- Vast lid

- Berichten: 52
- Lid geworden op: 25 apr 2007, 17:09
- Locatie: genk
Bericht
door jogo » 17 mar 2013, 12:52
De zijde kan een maximum bereiken van 2 x 60 x cos (180/8) of 120.cos22,5°=A
In de (gelijkbenige) driehoek met basis A en hoogte 140 kunnen we schrijven (X/140-H )=(A/140) daar uit volgt X=(A/140).(140-H) , indien H=140 dan is X=0
Voor het volume (I) = X².H = ((A/140).(140-H))².H = ((120.cos22,5°/140).(140-H))².H
Het volume is nu in functie geschreven van de hoogte (met limieten H=140 en H=0 waarbij (I) = 0)
Ps. kunt ge hier ook tekeningetjes uploaden ?
-
jogo
- Vast lid

- Berichten: 52
- Lid geworden op: 25 apr 2007, 17:09
- Locatie: genk
Bericht
door jogo » 20 mar 2013, 16:00
Ik heb in een XL bestand uitgerekend welke de balkinhoud is voor hoogtes oplopend van 1 tot 139
, daaruit blijkt dat voor hoogte 46 de inhoud 254888.7406
is,voor hoogte 47 de inhoud 254918.2143 is en voor hoogte 48 de inhoud terug daalt naar 254773.3541
Dus de oplossing is een balk met een hoogte tussen 47 en 48.
(wetende dat deze oplossing hier (terecht) niet wordt aanvaard)
De inhoud waarden volgen een mooie curve, waarvan ge de top zou moeten kunnen berekenen.(die kennis is blijkbaar bij mij verloren gegaan,jammer...)
-
Rmo
- Vast lid

- Berichten: 58
- Lid geworden op: 28 feb 2013, 18:30
Bericht
door Rmo » 21 mar 2013, 09:03
Is dit niet gewoon een kwestie van h uit te drukken in functie van x, dan de functie f(x)=x^2*h te beschouwen en daar het maximum van te zoeken?
-
meneer van Hoesel
- Vergevorderde

- Berichten: 395
- Lid geworden op: 20 apr 2010, 14:43
- Locatie: Zwolle
Bericht
door meneer van Hoesel » 23 mar 2013, 15:20
jogo schreef:Ik heb in een XL bestand uitgerekend welke …
Dus de oplossing is een balk met een hoogte tussen 47 en 48.
wetende dat deze oplossing hier (terecht) niet wordt aanvaard
Och... het ligt er aan hoe je er tegen aan kijkt, op VMBO wordt zo'n methode 'inklemmen genoemd' en er worden wel vaker numerieke antwoorden geaccepteerd, numerieke wiskunde is een vak opzicht.
Het venijn zit in de vraagstelling, 'zoek uit welke waarden van…' en 'bereken deze maximale inhoud'. Maar er staat ook 'Laat zien hoe…'
Als aanvulling op jouw excell oplossing die best acceptabel is, als je dan al weet dat de hoogte tussen de 47 en 48 ligt, waarom vul je de spreadsheet niet opnieuw met getallen opklimmend van 47.00 t/m 47.99 - en als je het antwoord in 4 cijfers nauwkeurig wil hebben, kun je dat nog eens een keer herhalen met de reeks die je dan hebt gevonden.
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 07 nov 2015, 13:17
viewtopic.php?f=28&t=8246
@bjornbuitink
Neem aan dat je op hoogte h in de pyramide een doorsnede bekijkt loodrecht de hoogtelijn, wat zie je dan ...
Je kan een tekening maken (dat is direct duidelijk) maar het is ook mogelijk de tekening eenvoudig (in woorden) te beschrijven ...
Verder bekijken we een verticale doorsnede bepaald door een diagonaalvlak van pyramide en blok ... , wat zie je?






