Hier kom ik niet uit, herschrijven van bvb
Herschrijf functie
Herschrijf functie
Herschrijf:  = 1 - \cos 2x - \sin^2 x) in de vorm
in de vorm  = a + b \cos(cx))
Hier kom ik niet uit, herschrijven van bvb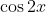 als
als 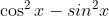 etc levert, vooralsnog niet op. Wat is een goede eerste stap?
etc levert, vooralsnog niet op. Wat is een goede eerste stap?
Hier kom ik niet uit, herschrijven van bvb
Re: Herschrijf functie
f(x)=sin^2(x)
Laat dat zien, daarna is de omvorming standaard nl herschrijven van het kwadraat naar a+bcos(2x) ...
Laat dat zien, daarna is de omvorming standaard nl herschrijven van het kwadraat naar a+bcos(2x) ...
Re: Herschrijf functie
ja daar ben ik o.a. op uitgekomen,
 - sin^2(x)) -sin^2(x))
=
 + sin^2(x) - sin^2(x))
=
)
=
)
maar wat dan?
=
=
=
maar wat dan?
Re: Herschrijf functie
Je kan (zoals ik zei) sin^2(x) omzetten in a+bcos(2x) ...
Welke formules ken je voor cos(2x) ...
Welke formules ken je voor cos(2x) ...
Re: Herschrijf functie
Heb even moeten zoeken, wist niet dat dit een standaard identiteit is.
Kreeg hem zelf niet afgeleid http://www.sosmath.com/trig/Trig5/trig5/trig5.html
Edit: eigenliji had ik het wel.af kunnen leiden, heb nameliji wel sqrt(1/2(1 +- cos (2x)) gebruikt
Kreeg hem zelf niet afgeleid http://www.sosmath.com/trig/Trig5/trig5/trig5.html
Edit: eigenliji had ik het wel.af kunnen leiden, heb nameliji wel sqrt(1/2(1 +- cos (2x)) gebruikt
Laatst gewijzigd door sebuts op 28 dec 2015, 13:14, 1 keer totaal gewijzigd.
Re: Herschrijf functie
Ok, succes verder!

