nulpunten van derdegraadsvergelijking

Mathhtam · Bericht door **Mathhtam** » 23 jul 2016, 17:21

Hallo!

Kan iemand me helpen met het vinden van de nulpunten van deze functie op een algebraïsche manier?
${x}^{3}+{x}^{2}+{x}^{1}+\frac{1}{3}=0$

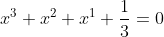
Alvast bedankt!

Bericht door **SafeX** » 23 jul 2016, 18:33

Wat heb je zelf bedacht ...

Mathhtam · Bericht door **Mathhtam** » 23 jul 2016, 19:06

De hoofstelling van de algebra gebruiken met de
nulpunten als onbekenden (1 nulpunt in dit geval). Vervolgens het uitwerken en de coëfficiënten van de gegeven functie gelijkstellen aan de coëfficiënten van het uitgewerkte en dan zo een stelsel oplossen.Heb wel iets gelezen van Cardano, maar die methode wordt in België precies niet gegeven aan scholieren

Is het mogelijk om dit op te lossen met dat stelsel?

Bericht door **SafeX** » 23 jul 2016, 19:22

Ok, waarom weet je dat er (maar) één nulpunt is ...
Cardano hoort niet in jullie 'bagage', dus wat is de bedoeling van deze opgave ...

Mathhtam · Bericht door **Mathhtam** » 23 jul 2016, 19:56

$f(x)={x}^{3}+{x}^{2}+{x}$ ontbonden in factoren geeft dat: ${x}\left ( {x}^{2}+{x}+1 \right )$ dus 1 nulpunt en vergeleken met de functie uit de opgave, is de functie verschoven naar boven.. in dit geval nog altijd 1 nulpunt.
De opgave stond tussen de opgaven met de bijhorende theorie (regel van Horner, afzondering van een gemeenschappelijke term, hoofdstelling van de algebra... algemeen: ontbinden in factoren)

Bericht door **SafeX** » 23 jul 2016, 20:08

Ok, tussen welke x-waarden ligt het nulpunt en waarom ...

Mathhtam · Bericht door **Mathhtam** » 23 jul 2016, 20:43

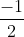
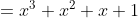
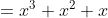
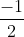
De x waarde zal een klein beetje groter zijn dan $\frac{-1}{2}$ , want f(x) + $\frac{2}{3}$ ( $= x^3 + x^2 + x + 1$ ) heeft duidelijk -1 als nulpunt en f(x) - $\frac{1}{3}$ ( $= x^3 + x^2 + x$ ) heeft nul als nulpunt. $\frac{1}{3}$ (de laatste term van de opgave functie f(x)) leunt het dichts bij het laatste functievoorschrift dus waarschijnlijk ietsje groter dan $\frac{-1}{2}$ ofzoiets ..

Bericht door **SafeX** » 23 jul 2016, 20:59

Voor het nulpunt (noem dit a) geldt: -1<a<0 en een volgende benadering is -.4<a<-.5 nu kan je met een RM zo verder gaan, maar is dat de bedoeling ... , Wat kan je voor ontbinding schrijven met x=a als nulpunt?

Heb je een GRM?

Mathhtam · Bericht door **Mathhtam** » 23 jul 2016, 21:43

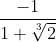
ik heb een GRM, maar vanaf hier weet ik niet hoe het verder moet.. het antwoord zou $\frac{-1}{1+ \sqrt[3]{2}}$ zijn volgens het boek. Er staat niet bij hoe men eraan komt

Bericht door **SafeX** » 24 jul 2016, 08:57

Ok, deze verg kan met jouw middelen algebraïsch worden opgelost ...

Vermenigvuldig met 3, schrijf dan:

$2x^3+x^3+3x^2+3x+1=0$

$x^3+3x^2+3x+1=-2x^3$

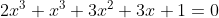
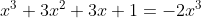
Het linkerlid is te schrijven als een derde macht van (...), dus (...)^3 , herken je dat?

Mathhtam · Bericht door **Mathhtam** » 24 jul 2016, 09:12

Het kan geschreven worden als $(X-1)^{3} = -2x^{3}$ dan de derdemachtswortel ofzoiets nemen van zowel linker als rechterlid en x isoleren ... Dankuwel!!

Bericht door **SafeX** » 24 jul 2016, 09:19

Nee, links staat (x+1)^3 ...

Deel nu, links en rechts, door x^3 ...

Mathhtam · Bericht door **Mathhtam** » 24 jul 2016, 09:47

$\left ( x+1 \right )^{3}=-2x^{3}$
$x+1= \sqrt[3]{-2}x$
$x-\sqrt[3]{-2}x=-1$
$x(1-\sqrt[3]{-2})=-1$
$x= \frac{-1}{1+\sqrt[3]{2}}$
stapgewijs zoiets?

Bericht door **SafeX** » 24 jul 2016, 10:06

Mathhtam schreef: $\left ( x+1 \right )^{3}=-2x^{3}$
$x+1= \sqrt[3]{-2}x=-\sqrt[3]{2}x=$
$x+\sqrt[3]{2}x=-1$
$x(1+\sqrt[3]{2})=-1$
$x= \frac{-1}{1+\sqrt[3]{2}}$

Wiskundeforum

nulpunten van derdegraadsvergelijking

nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking

Re: nulpunten van derdegraadsvergelijking