Logaritmen
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Logaritmen
Hallo allemaal,
Ik ben bezig met mijn huiswerk uit het hoofdstuk logaritmen, hierin komt de volgende som voor :
x^1.2 = 4
de vraag: Los op in R en benader de uitkomst in 3 decimalen nauwkeurig .
Ik heb de som zo uitgewerkt:
x^1.2 = x^10/12 = x^5/6 = 4
=> x= 4^5/6
=> x= 3 ,175
Is mijn uitwerking juist? Of heb ik iets te gemakkelijk naar het antwoord toegewerkt ? ( alleen het antwoord is gegeven in ons dictaat )
Alvast bedankt voor jullie hulp.
Ik ben bezig met mijn huiswerk uit het hoofdstuk logaritmen, hierin komt de volgende som voor :
x^1.2 = 4
de vraag: Los op in R en benader de uitkomst in 3 decimalen nauwkeurig .
Ik heb de som zo uitgewerkt:
x^1.2 = x^10/12 = x^5/6 = 4
=> x= 4^5/6
=> x= 3 ,175
Is mijn uitwerking juist? Of heb ik iets te gemakkelijk naar het antwoord toegewerkt ? ( alleen het antwoord is gegeven in ons dictaat )
Alvast bedankt voor jullie hulp.
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen
Je gaat al de fout in bij het omschrijven van 1,2 naar een gewone breuk. Je hebt namelijk de teller en de noemer verwisseld, dus er moet gelden dat 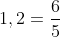 . Je zoekt dus die x waarvoor
. Je zoekt dus die x waarvoor 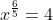 . Maak nu eens gebruik van de eigenschap dat
. Maak nu eens gebruik van de eigenschap dat ^n=x^{m\cdot n}) om de vergelijking in de gedaante x = ... te schrijven.
om de vergelijking in de gedaante x = ... te schrijven.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
Oke als ik het goed begrijp ;
x^5/6 = 4^1 (^1 schrijf je normaal niet )
=> x= 4 ^5/5 / ^6/5
=> 5/5 * 5/6 = 25/30 = 5/6 ( vermenigvuldigen met het omgekeerde )
=> x = 4 ^5/6
x^5/6 = 4^1 (^1 schrijf je normaal niet )
=> x= 4 ^5/5 / ^6/5
=> 5/5 * 5/6 = 25/30 = 5/6 ( vermenigvuldigen met het omgekeerde )
=> x = 4 ^5/6
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen
Merk op dat een breuk met dezelfde teller en noemer altijd de waarde 1 heeft, zodat je directWesterwolde schreef:Oke als ik het goed begrijp ;
x^5/6 = 4^1 (^1 schrijf je normaal niet )
=> x= 4 ^5/5 / ^6/5
=> 5/5 * 5/6 = 25/30 = 5/6 ( vermenigvuldigen met het omgekeerde )
Dat is inderdaad het juiste antwoord.Westerwolde schreef:=> x = 4 ^5/6
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
arno schreef:Merk op dat een breuk met dezelfde teller en noemer altijd de waarde 1 heeft, zodat je directWesterwolde schreef:Oke als ik het goed begrijp ;
x^5/6 = 4^1 (^1 schrijf je normaal niet )
=> x= 4 ^5/5 / ^6/5
=> 5/5 * 5/6 = 25/30 = 5/6 ( vermenigvuldigen met het omgekeerde )kunt schrijven.
Ohja idd dat was me niet opgevallen.
Dat is inderdaad het juiste antwoord.Westerwolde schreef:=> x = 4 ^5/6
Vriendelijk bedankt voor je hulp.
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
Even verderop heb ik volgende som:
x ^√2 = 2
Die heb ik op de volgende manier uitgewerkt, maar dit komt niet overeen met het antwoordenblad, wat gaat hier mis ?
x ^√2 = 2
=> x ^1/2 = 2
=> x = 2 ^2/2 / 1/2 = ^2/2 * 2/1 = 2/1
=> x= 2 ^2/1
x ^√2 = 2
Die heb ik op de volgende manier uitgewerkt, maar dit komt niet overeen met het antwoordenblad, wat gaat hier mis ?
x ^√2 = 2
=> x ^1/2 = 2
=> x = 2 ^2/2 / 1/2 = ^2/2 * 2/1 = 2/1
=> x= 2 ^2/1
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen
Als 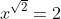 kun je hetzelfde principe toepassen als bij de vorige vraag. Stel in
kun je hetzelfde principe toepassen als bij de vorige vraag. Stel in ^n=x^{m\cdot n}) m = n = √2. Lukt het je nu wel om de juiste waarde voor x te vinden?
m = n = √2. Lukt het je nu wel om de juiste waarde voor x te vinden?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
arno schreef:Alskun je hetzelfde principe toepassen als bij de vorige vraag. Stel in
m = n = √2. Lukt het je nu wel om de juiste waarde voor x te vinden?
Ik kom maar steeds weer uit op die x= 2 ^2/1 , ik zie het blijkbaar echt niet. Kun je me de volgende stap op weg helpen ?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen
Je weet datWesterwolde schreef:arno schreef:Alskun je hetzelfde principe toepassen als bij de vorige vraag. Stel in
m = n = √2. Lukt het je nu wel om de juiste waarde voor x te vinden?
Ik kom maar steeds weer uit op die x= 2 ^2/1 , ik zie het blijkbaar echt niet. Kun je me de volgende stap op weg helpen ?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
arno schreef:Je weet datWesterwolde schreef:arno schreef:Alskun je hetzelfde principe toepassen als bij de vorige vraag. Stel in
m = n = √2. Lukt het je nu wel om de juiste waarde voor x te vinden?
Ik kom maar steeds weer uit op die x= 2 ^2/1 , ik zie het blijkbaar echt niet. Kun je me de volgende stap op weg helpen ?, dus
, dus x = √2
Klopt dit?
Re: Logaritmen
Je vindt:Westerwolde schreef:Klopt dit?
x = √2
Dus, zou:
Je kan dit met je RM narekenen ...
Probeer het eens met √2=2^(1/2) ...
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
SafeX schreef:Je vindt:Westerwolde schreef:Klopt dit?
x = √2
Dus, zou:
Je kan dit met je RM narekenen ...
Probeer het eens met √2=2^(1/2) ...
Uit: √2^(√2) = 1, 632
Uit: √2^(1/2) = 1, 414
Is √2^(√2) het antwoord al ?
Re: Logaritmen
Je zou 2 moeten krijgen ...
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen
SafeX schreef:Je zou 2 moeten krijgen ...
Zie mijn afbeelding :
https://myalbum.com/album/no1vJwfMBqZB
Re: Logaritmen
Ja, die RM doet het goed, maar dat bedoel ik niet ...Westerwolde schreef:Zie mijn afbeelding
Je opgave is:
Jij vindt: een antwoord, dan moet je na invullen 2 krijgen. Eens?Westerwolde schreef:x ^√2 = 2
Ga eerst na: x is een grondtal. Probeer eens x=1 ook x=2, lukt het op die manier? Kan je x schatten?
Hoe nu: je wilt x^1, eens?
Tot welke macht moet je x^√2 verheffen om x^1 te krijgen.
Bekijk: (x^√2)^p=x^(...)= ...
