Logaritmen bereken x
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Logaritmen bereken x
Hallo allemaal,
Ik ben bezig met mijn huiswerk uit het hoofdstuk logaritmen, hierin komt de volgende som voor :
bereken x uit : ^4log(25) = ^8log(x)
Hoe pak ik dergelijke som aan ?
Ik ben bezig met mijn huiswerk uit het hoofdstuk logaritmen, hierin komt de volgende som voor :
bereken x uit : ^4log(25) = ^8log(x)
Hoe pak ik dergelijke som aan ?
Re: Logaritmen bereken x
Ken je de definitie van de logaritme?
Ken je de RR voor het werken met logaritmen? Zo ja, je moet de vierde RR gebruiken ...
Ken je de RR voor het werken met logaritmen? Zo ja, je moet de vierde RR gebruiken ...
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen bereken x
Ja dat is : ^g log a = x <=> g^x = a
Ik ken meerdere rekenregels voor logaritmen, bedoel je onderstaande met de vierde ?
^g log (a) = ^p log (a) / ^p log (g) ?
Of ^p log (a^n) = n^p log (a) ?
Ik ken meerdere rekenregels voor logaritmen, bedoel je onderstaande met de vierde ?
^g log (a) = ^p log (a) / ^p log (g) ?
Of ^p log (a^n) = n^p log (a) ?
Re: Logaritmen bereken x
Kies voor p=2 ...Westerwolde schreef:^g log (a) = ^p log (a) / ^p log (g)
kan je na deze keuze zien waarom je 2 kiest
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen bereken x
SafeX schreef:Kies voor p=2 ...Westerwolde schreef:^g log (a) = ^p log (a) / ^p log (g)
kan je na deze keuze zien waarom je 2 kiest
Oke dan krijgen we: ^g log (a) = ^2 log (a) / ^2 log (g)
Ik zie niet waarom we 2 kiezen, maar ik zie wel dat deze twee grondtallen gelijk zijn ..
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen bereken x
Stel 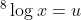 , dan geldt dat
, dan geldt dat ^u=2^{3u}=x) , dus 3u = ..., dus u = ... Stel
, dus 3u = ..., dus u = ... Stel 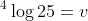 , dan geldt dat
, dan geldt dat ^v=2^{2v}=25) , dus 2v = ..., dus v = ... Wat is dus de gezochte waarde van x?
, dus 2v = ..., dus v = ... Wat is dus de gezochte waarde van x?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen bereken x
arno schreef:Stel, dan geldt dat
, dus 3u = 8, dus u = 5 Stel
, dan geldt dat
, dus 2v = 4, dus v = 2 Wat is dus de gezochte waarde van x?
Ik heb wat ingevuld, maar ik durf niet met zekerheid te zeggen dat ik er achter kan staan..
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen bereken x
Bedenk dat uitWesterwolde schreef:arno schreef:Stel, dan geldt dat
, dus 3u = 8, dus u = 5 Stel
, dan geldt dat
, dus 2v = 4, dus v = 2 Wat is dus de gezochte waarde van x?
Ik heb wat ingevuld, maar ik durf niet met zekerheid te zeggen dat ik er achter kan staan..
en uit
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Logaritmen bereken x
Mooi, wat zegt deze definitie ...Westerwolde schreef:Ja dat is : ^g log a = x <=> g^x = a
Eigenlijk staat er een verg met een log gelijk aan x, rechts staat ook een verg met x in de exponent, maw een log is een exponent!
Begrijp je dit? Zo ja geef commentaar ...
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen bereken x
arno schreef:Bedenk dat uitWesterwolde schreef:arno schreef:Stel, dan geldt dat
, dus 3u = 8, dus u = 5 Stel
, dan geldt dat
, dus 2v = 4, dus v = 2 Wat is dus de gezochte waarde van x?
Ik heb wat ingevuld, maar ik durf niet met zekerheid te zeggen dat ik er achter kan staan..volgt dat
, dus uit
volgt dat 3u = ..., dus u = ...
en uitvolgt dat 2v = ..., dus v = ... Bepaal nu x als je weet dat u = v.
Als ik het goed begrijp moet ik openstaande punten zo invullen ;
2^3u = x => 3u = ^2log(x) => v= ^2log 3
2^2v = 25 => 2v= ^2log 25 => v= ^2log 25
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen bereken x
SafeX schreef:Mooi, wat zegt deze definitie ...Westerwolde schreef:Ja dat is : ^g log a = x <=> g^x = a
Eigenlijk staat er een verg met een log gelijk aan x, rechts staat ook een verg met x in de exponent, maw een log is een exponent!
Begrijp je dit? Zo ja geef commentaar ...
Wat deze definitie zegt lukt me niet om in woorden uit te drukken, maar ik kan een voorbeeld geven;
2log 8 = 3 <=> 2^3 = 8
Ja ik begrijp je uitleg.
Re: Logaritmen bereken x
Als je nu links en rechts RR 4 toepast met p=2, wat komt er dan te staan ...Westerwolde schreef:bereken x uit : ^4log(25) = ^8log(x)
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Logaritmen bereken x
SafeX schreef:Als je nu links en rechts RR 4 toepast met p=2, wat komt er dan te staan ...Westerwolde schreef:bereken x uit : ^4log(25) = ^8log(x)
Links:
^g log (a) = ^p log (a) / ^p log (g)
=> ^2log(a) / ^2log(g)
=> ^2log(25) / ^2log(2)
Rechts:
^g log (a) = ^p log (a) / ^p log (g)
=> ^2log(a) / ^2log(g)
=> ^2log(x) / ^2log(8)
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen bereken x
Nee, g is links 4, dus je moet delen door... Welk getal krijg je dan?Westerwolde schreef:Links:
^g log (a) = ^p log (a) / ^p log (g)
=> ^2log(a) / ^2log(g)
=> ^2log(25) / ^2log(2)
Dit klopt wel. Wat is de waarde vanWesterwolde schreef:Rechts:
^g log (a) = ^p log (a) / ^p log (g)
=> ^2log(a) / ^2log(g)
=> ^2log(x) / ^2log(8)
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Logaritmen bereken x
Dit klopt, dus u = ⅓∙3u = ...Westerwolde schreef:arno schreef: Bedenk dat uitvolgt dat
, dus uit
volgt dat 3u = ..., dus u = ...
en uitvolgt dat 2v = ..., dus v = ... Bepaal nu x als je weet dat u = v.
Als ik het goed begrijp moet ik openstaande punten zo invullen ;
2^3u = x => 3u = ^2log(x)
Dit klopt, dus v = ½∙v = ... Bepaal nu x als je weet dat u = v.Westerwolde schreef:2^2v = 25 => 2v= ^2log 25
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
