Gemiddelde vinden met gegeven pecentielen P10 en P90
Gemiddelde vinden met gegeven pecentielen P10 en P90
In een opgave wordt o.a. gevraagd het gemiddelde te berekenen van de lengte van 21-jarige jongens. Er geld dat de lengte van 21 jarige jongens normaal verdeeld is en dat p10 = 174 cm en p90 = 190 cm. In kwam er niet uit en vond in de uitwerkingen dat het gemiddelde te vinden valt door de twee maten bij de percentielen op te tellen en vervolgens de delen door 2; ik heb echter moeite mee om te begrijpen waarom dit zo is. Zoals ik het nu beredeneer liggen bij P10 10% van alle lengtes onder deze waarde (174 cm), en liggen bij P90 90% van alle lengtes onder deze waarde (190 cm). Waarom levert de optelsom van deze twee waarden een gemiddelde (P50) op?
Re: Gemiddelde vinden met gegeven pecentielen P10 en P90
Gebruik:
- p10 = 174 betekent dat 10% van de metingen <= 174 is
- P90 = 190 betekent dat 90% van de metingen <= 190 is, dus 10% > 190
- De grafiek van de normale verdeling (= de klokcurve) is symmetrisch ten opzichte van de lijn "x = gemiddelde".
Kom je hiermee verder?
(maak zo nodig een schets van de klokcurve en teken de bovenstaande gegevens daar in)
- p10 = 174 betekent dat 10% van de metingen <= 174 is
- P90 = 190 betekent dat 90% van de metingen <= 190 is, dus 10% > 190
- De grafiek van de normale verdeling (= de klokcurve) is symmetrisch ten opzichte van de lijn "x = gemiddelde".
Kom je hiermee verder?
(maak zo nodig een schets van de klokcurve en teken de bovenstaande gegevens daar in)
Re: Gemiddelde vinden met gegeven pecentielen P10 en P90
Bedankt. Ik heb het uitgetekend, en Ik snap in principe wat u zegt en denk dat ik het nu misschien begrijp, maar zoek voor mijn redenering bevestiging. Moet ik het me zo voorstellen:
-p10: links ligt 10% van de data, rechts ligt 90% van de data.
-p90: links ligt 90% van de data, rechts ligt 10% van de data.
- Beide punten (p10 en p90) liggen “symmetrisch” in verhouding tot elkaar. (Ik weet niet goed hoe ik dit moet uitdrukken; wat ik bedoel is dat de afstanden tussen de punten p10 en p90; en de afstanden tussen p0 en p10 en p90 p100 een zekere symmetrie vertonen omdat de klokcurve per definitie een volledig symmetrisch verdeeld curve is)
- Twee van deze punten opgeteld en dan gedeeld door 2 levert het gemiddelde (μ) op.
Als dit zo is; klopt het dan ook dat bijvoorbeeld: (p20+p80)/2=μ en (p2+p98)/2=μ?
-p10: links ligt 10% van de data, rechts ligt 90% van de data.
-p90: links ligt 90% van de data, rechts ligt 10% van de data.
- Beide punten (p10 en p90) liggen “symmetrisch” in verhouding tot elkaar. (Ik weet niet goed hoe ik dit moet uitdrukken; wat ik bedoel is dat de afstanden tussen de punten p10 en p90; en de afstanden tussen p0 en p10 en p90 p100 een zekere symmetrie vertonen omdat de klokcurve per definitie een volledig symmetrisch verdeeld curve is)
- Twee van deze punten opgeteld en dan gedeeld door 2 levert het gemiddelde (μ) op.
Als dit zo is; klopt het dan ook dat bijvoorbeeld: (p20+p80)/2=μ en (p2+p98)/2=μ?
Re: Gemiddelde vinden met gegeven pecentielen P10 en P90
Wat netter uitgedrukt:Jacko1996 schreef:- Beide punten (p10 en p90) liggen “symmetrisch” in verhouding tot elkaar. (Ik weet niet goed hoe ik dit moet uitdrukken; wat ik bedoel is dat de afstanden tussen de punten p10 en p90; en de afstanden tussen p0 en p10 en p90 p100 een zekere symmetrie vertonen omdat de klokcurve per definitie een volledig symmetrisch verdeeld curve is)
Bij een symmetrische kansverdelingsfunctie (zoals die van de normale verdeling) liggen p10 en p90 even ver maar aan weerszijden van p50 = mediaan (= gemiddelde bij een symmetrische kansverdeling)
Klopt.Jacko1996 schreef: Als dit zo is; klopt het dan ook dat bijvoorbeeld: (p20+p80)/2=μ en (p2+p98)/2=μ?
Het gemiddelde μ van de symmetrische verdeling
= "het punt dat precies tussen p[n] en p[100-n] in ligt"
= het gemiddelde van p[n] en p[100-n]
= (p[n]+p[100-n]) / 2
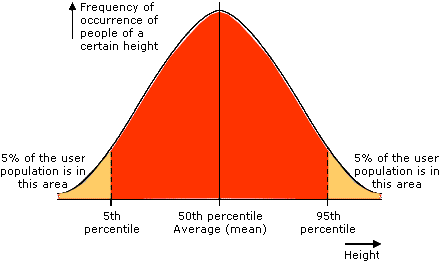
Hier nog een plaatje van internet voor de verdeling van de lichaamslengte (height) met daarin aangegeven p5, p95 en p50=mediaan (vanwege de symmetrie is mediaan = gemiddelde (mean)):
Re: Gemiddelde vinden met gegeven pecentielen P10 en P90
Erg bedankt; ik begrijp het nu.
Re: Gemiddelde vinden met gegeven pecentielen P10 en P90
Mooi!
PS: ik heb je volledige "Quotes" verwijderd, dat spaart ruimte en verhoogt de leesbaarheid.
Je kan de knop "Reageer" (links onder in elk forum-onderwerp) gebruiken om een bericht toe te voegen.
Handig om te weten als je weer vragen hebt (altijd welkom).
PS: ik heb je volledige "Quotes" verwijderd, dat spaart ruimte en verhoogt de leesbaarheid.
Je kan de knop "Reageer" (links onder in elk forum-onderwerp) gebruiken om een bericht toe te voegen.
Handig om te weten als je weer vragen hebt (altijd welkom).
Re: Gemiddelde vinden met gegeven pecentielen P10 en P90
Oké; ik zal er in de toekomst rekening mee houden. Ik gebruikte de quote optie omdat ik onder de impressie was dat dit wellicht een notificatie oplevert bij de gequote. Ik kan me vanuit het perspectief van een toekomstig lezer echter voorstellen dat het de pagina's behoorlijk opvult.

