Afgeleide goniometrische functie
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Afgeleide goniometrische functie
Hallo,
Ik ben bezig met het bepalen van de afgeleide van een aantal goniometrische functies.
Sommige sommen kom ik wel uit,maar bij een aantal loop ik vast, onder andere de volgende;
f(x)= 1+tan(x) / 1-tan(x)
ik maak gebruik van de formule: y= u/v => y'= v*u' - u*v' / v^2
f'(x) =(1-tan(x)) * 1/cos^2(x) - (1-cos(x) * - 1/cos^2(x) / (1 - tan(x)^2
=> 1-tan(x) * 1-(1-cos(x)) -1 / (1-tan(x))^2 *cos^2(x)
=> -tan(x)+cos(x) + 2 / (1 - tan(x))^2 * cos^2(x)
vanaf het laatste punt kom ik verder, wie kan me daar bij helpen ?
Ik ben bezig met het bepalen van de afgeleide van een aantal goniometrische functies.
Sommige sommen kom ik wel uit,maar bij een aantal loop ik vast, onder andere de volgende;
f(x)= 1+tan(x) / 1-tan(x)
ik maak gebruik van de formule: y= u/v => y'= v*u' - u*v' / v^2
f'(x) =(1-tan(x)) * 1/cos^2(x) - (1-cos(x) * - 1/cos^2(x) / (1 - tan(x)^2
=> 1-tan(x) * 1-(1-cos(x)) -1 / (1-tan(x))^2 *cos^2(x)
=> -tan(x)+cos(x) + 2 / (1 - tan(x))^2 * cos^2(x)
vanaf het laatste punt kom ik verder, wie kan me daar bij helpen ?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Afgeleide goniometrische functie
Wellicht is het handiger om eerst een en ander wat te herschrijven. Zo is 1+tan x = 1-tan x+2tan x, dus 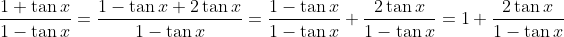 . Differentieer nu
. Differentieer nu 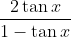 om tot het gevraagde antwoord te komen. Merk op dat als tan x = u betekent dat de teller als 2u en de noemer als 1-u te schrijven is. Wat is dan de afgeleide van de teller, wat is dan de afgeleide van de noemer, dus wat wordt dan de uiteindelijke afgeleide?
om tot het gevraagde antwoord te komen. Merk op dat als tan x = u betekent dat de teller als 2u en de noemer als 1-u te schrijven is. Wat is dan de afgeleide van de teller, wat is dan de afgeleide van de noemer, dus wat wordt dan de uiteindelijke afgeleide?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
arno schreef:Wellicht is het handiger om eerst een en ander wat te herschrijven. Zo is 1+tan x = 1-tan x+2tan x, dus. Differentieer nu
om tot het gevraagde antwoord te komen. Merk op dat als tan x = u betekent dat de teller als 2u en de noemer als 1-u te schrijven is. Wat is dan de afgeleide van de teller, wat is dan de afgeleide van de noemer, dus wat wordt dan de uiteindelijke afgeleide?
Aha daar ging het dus al mis bij mij.
Als ik het nu goed begrijp is de volgende stap:
1-tan(x) * 2/cos^2(x) - (2tan(x)) * - 1/cos^2(x) / 1-tan(x) ^ 2
Klopt het tot zo ver ?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Afgeleide goniometrische functie
De uitwerking van de teller klopt tot zover, maar de noemer niet. Waaraan is (a-b)² gelijk? Wat wordt dus de uitdrukking voor de noemer?Westerwolde schreef:Aha daar ging het dus al mis bij mij.
Als ik het nu goed begrijp is de volgende stap:
1-tan(x) * 2/cos^2(x) - (2tan(x)) * - 1/cos^2(x) / 1-tan(x) ^ 2
Klopt het tot zo ver ?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
arno schreef:De uitwerking van de teller klopt tot zover, maar de noemer niet. Waaraan is (a-b)² gelijk? Wat wordt dus de uitdrukking voor de noemer?Westerwolde schreef:Aha daar ging het dus al mis bij mij.
Als ik het nu goed begrijp is de volgende stap:
1-tan(x) * 2/cos^2(x) - (2tan(x)) * - 1/cos^2(x) / 1-tan(x) ^ 2
Klopt het tot zo ver ?
(a-b)^2 = (a+b)(a-b)
1-tan(x) * 2/cos^2(x) - (2tan(x)) * - 1/cos^2(x) / 1+tan(x) * 1-tan(x)
Is nu de volgende stap cos^2(x) uit de teller vermenigvuldigen ?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Afgeleide goniometrische functie
Dit is fout. Bedenk dat (a-b)² = (a-b)(a-b) = a(a-b)-b(a-b) = ...Westerwolde schreef:(a-b)^2 = (a+b)(a-b)
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
arno schreef:Dit is fout. Bedenk dat (a-b)² = (a-b)(a-b) = a(a-b)-b(a-b) = ...Westerwolde schreef:(a-b)^2 = (a+b)(a-b)
(a-b)^2 = a^2 - 2ab + b^2
In dat geval geldt voor de noemer: 1-2tan(x) + tan^2(x)
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Afgeleide goniometrische functie
Dat klopt. Je kunt de noemer laten staan als (1-tan x)². Wat vind je als uiteindelijke waarde voor de teller, dus wat wordt de uiteindelijke afgeleide?Westerwolde schreef:(a-b)^2 = a^2 - 2ab + b^2
In dat geval geldt voor de noemer: 1-2tan(x) + tan^2(x)
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
arno schreef:Dat klopt. Je kunt de noemer laten staan als (1-tan x)². Wat vind je als uiteindelijke waarde voor de teller, dus wat wordt de uiteindelijke afgeleide?Westerwolde schreef:(a-b)^2 = a^2 - 2ab + b^2
In dat geval geldt voor de noemer: 1-2tan(x) + tan^2(x)
=> 1-tan(x)*2 - (2tan(x)*(-1) /
(1-tan(x))^2 (cos(x))^2
=> 2-tan(x) + 2 tan(x) /
(1-tan(x))^2 (cos(x))^2
=> 2 /
(1-tan(x))^2 (cos(x))^2
Kunnen we nog iets aan de noemer wijzigen ?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Afgeleide goniometrische functie
Je krijgt als uiteindelijke afgeleide inderdaad ^2\cos^2x}) . Merk op dat dit te herschrijven is als
. Merk op dat dit te herschrijven is als }{(1-\tan x)^2}) , wat het uiteindelijke resultaat van de afgeleide is.
, wat het uiteindelijke resultaat van de afgeleide is.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
arno schreef:Je krijgt als uiteindelijke afgeleide inderdaad. Merk op dat dit te herschrijven is als
, wat het uiteindelijke resultaat van de afgeleide is.
Ik zie dat ik ook een kwadraat te veel had in de noemer bij cos(x)
Maar hoe raak jij die cos^2(x) kwijt in de noemer ?
Re: Afgeleide goniometrische functie
Allereerst bedoel je hier: f(x)= [1+tan(x)] /[1-tan(x)]Westerwolde schreef: f(x)= 1+tan(x) / 1-tan(x)
Ik gebruik hier vierkante haken om het sterker te benadrukken, Geen haakjes gebruiken is foutief, ga dat na!
De 'vereenvoudiging' van arno is, hoe goed bedoeld, onnodig en niet besparend.
Ik geef de verbeteringen aan:f'(x) =(1-tan(x)) * 1/cos^2(x) - (1-cos(x) * - 1/cos^2(x) / (1 - tan(x)^2
=> 1-tan(x) * 1-(1-cos(x)) -1 / (1-tan(x))^2 *cos^2(x)
=> -tan(x)+cos(x) + 2 / (1 - tan(x))^2 * cos^2(x)
f'(x) =[(1-tan(x)) * 1/cos^2(x) - (1+tan(x)) * - 1/cos^2(x)] / (1 - tan(x))^2
Dit leidt direct na haakjes verdrijven in de teller tot:
=> 2 /[(1-tan(x))^2 *cos^2(x)]= 2/[(1-tan(x))cos(x)]^2
Als je het product van de noemer bepaalt krijg je het 'gewenste' antwoord.
Bepaal ook nog het domein van f(x) en f'(x)
=> -tan(x)+cos(x) + 2 / (1 - tan(x))^2 * cos^2(x)
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
SafeX schreef:Allereerst bedoel je hier: f(x)= [1+tan(x)] /[1-tan(x)]Westerwolde schreef: f(x)= 1+tan(x) / 1-tan(x)
Ik gebruik hier vierkante haken om het sterker te benadrukken, Geen haakjes gebruiken is foutief, ga dat na!
De 'vereenvoudiging' van arno is, hoe goed bedoeld, onnodig en niet besparend.
Ik geef de verbeteringen aan:f'(x) =(1-tan(x)) * 1/cos^2(x) - (1-cos(x) * - 1/cos^2(x) / (1 - tan(x)^2
=> 1-tan(x) * 1-(1-cos(x)) -1 / (1-tan(x))^2 *cos^2(x)
=> -tan(x)+cos(x) + 2 / (1 - tan(x))^2 * cos^2(x)
f'(x) =[(1-tan(x)) * 1/cos^2(x) - (1+tan(x)) * - 1/cos^2(x)] / (1 - tan(x))^2
Dit leidt direct na haakjes verdrijven in de teller tot:
=> 2 /[(1-tan(x))^2 *cos^2(x)]= 2/[(1-tan(x))cos(x)]^2
Als je het product van de noemer bepaalt krijg je het 'gewenste' antwoord.
Bepaal ook nog het domein van f(x) en f'(x)
=> -tan(x)+cos(x) + 2 / (1 - tan(x))^2 * cos^2(x)
Ja oke duidelijk wat je hier boven beschrijft.
Als ik het goed begrijp kun je de noemer nog verder uit werken?
Het product van tan en cos is toch de sinus ?
Re: Afgeleide goniometrische functie
Precies, maar dat kan je zelf ook nauwkeurig uitschrijven (neem ik aan).Westerwolde schreef:Het product van tan en cos is toch de sinus ?
Hoe staat f'(x) in jouw antwoorden?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: Afgeleide goniometrische functie
SafeX schreef:Precies, maar dat kan je zelf ook nauwkeurig uitschrijven (neem ik aan).Westerwolde schreef:Het product van tan en cos is toch de sinus ?
Hoe staat f'(x) in jouw antwoorden?
(1 - tan(x))^2 * cos^2(x)
=> tan(x) = [sin(x)] / [cos(x)]
=> = [cos(x)] * [sin(x)] / [cos(x)] = [1-sin(x)]^2
=> [2] / [1-sin(x)]^2
Hm in het antwoordenboek staat : [2] / [1-sin(2x)]
