Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Dit forum is voor het voortgezetonderwijs (of 2de/3de graad ASO), als je in de bovenbouw zit. We gaan er vanuit dat je een Grafische Rekenmachine hebt.
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 08 mar 2017, 12:34
SafeX schreef:Westerwolde schreef:De eerste term bevat 3* een sin(x)
We zeggen: De eerste term bevat 3 factoren sin(x). Wat is het verschil?
Kan je nu verder? Wat wordt f'(x)?
Ja precies dat is een betere benaming.
f'(x) = [ sin(x)*sin(x) * -sin(x)] + [cos(x)* 2sin(x)*cos(x)]
Nu haal ik sin(x) uit beide termen. En omdat de eerste term 3 factoren sin(x) bevat, plaats
ik een 3 binnen de haken voor sin(x). ( is dit juiste beredeneerd? )
f'(x) = sin(x) ([2cos^2(x)] - [3sin^2(x)])
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 08 mar 2017, 12:41
Westerwolde schreef:En omdat de eerste term 3 factoren sin(x) bevat, plaats
ik een 3 binnen de haken voor sin(x). ( is dit juiste beredeneerd? )
Stel ik noteer a*a*a= ... , zijn dit 3 factoren a? Zo ja, hoe noteer je dit beknopt?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 08 mar 2017, 13:01
SafeX schreef:Westerwolde schreef:En omdat de eerste term 3 factoren sin(x) bevat, plaats
ik een 3 binnen de haken voor sin(x). ( is dit juiste beredeneerd? )
Stel ik noteer a*a*a= ... , zijn dit 3 factoren a? Zo ja, hoe noteer je dit beknopt?
Dat zou ik noteren als a^3. Dus voor die sin(x) moet ik geen 3 plaatsen..
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 08 mar 2017, 13:17
Westerwolde schreef:
Dat zou ik noteren als a^3.
Prima!
Dus voor die sin(x) moet ik geen 3 plaatsen..
Kan je deze vraag nu zelf beantwoorden? Zo nee, wat is er onduidelijk?
Vraag je ook af hoe je 3a zou kunnen schrijven.
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 08 mar 2017, 13:29
SafeX schreef:Westerwolde schreef:
Dat zou ik noteren als a^3.
Prima!
Dus voor die sin(x) moet ik geen 3 plaatsen..
Kan je deze vraag nu zelf beantwoorden? Zo nee, wat is er onduidelijk?
Vraag je ook af hoe je 3a zou kunnen schrijven.
3a = a+a+a
Terug naar onze som: f'(x) = sin(x) ([2cos^2(x)] - [sin^2(x)])
Dit is nog goed?
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 08 mar 2017, 13:58
Westerwolde schreef:
Terug naar onze som: f'(x) = sin(x) ([2cos^2(x)] - [sin^2(x)])
Dit is nog goed?
Ja, dit is goed, maar liever zie iken ik hoop ook jij zelf:
Westerwolde schreef:
f'(x) = [ sin(x)*sin(x) * -sin(x)] + [cos(x)* 2sin(x)*cos(x)]
Nu haal ik sin(x) uit beide termen.
en nu:
f'(x) = sin(x) (2cos^2(x) - sin^2(x))
Waarom, denk je heb ik de veelheid aan haakjes weggehaald.
En probeer nu toch ook maar de
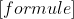
te gebruiken.
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 08 mar 2017, 14:19
SafeX schreef:Westerwolde schreef:
Terug naar onze som: f'(x) = sin(x) ([2cos^2(x)] - [sin^2(x)])
Dit is nog goed?
Ja, dit is goed, maar liever zie iken ik hoop ook jij zelf:
Westerwolde schreef:
f'(x) = [ sin(x)*sin(x) * -sin(x)] + [cos(x)* 2sin(x)*cos(x)]
Nu haal ik sin(x) uit beide termen.
en nu:
f'(x) = sin(x) (2cos^2(x) - sin^2(x))
Waarom, denk je heb ik de veelheid aan haakjes weggehaald.
En probeer nu toch ook maar de
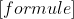
te gebruiken.
Daar wordt het iets duidelijker van zonder al die haakjes.
Welke formule moet ik gebruiken voor cos(x) - sin(x) ? Ik ken daar geen standaard formule voor
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 08 mar 2017, 14:31
Westerwolde schreef:Welke formule moet ik gebruiken voor cos(x) - sin(x) ? Ik ken daar geen standaard formule voor
Dat zie ik niet staan!
Naar welk antwoord zoek je nu?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 08 mar 2017, 14:57
SafeX schreef:Westerwolde schreef:Welke formule moet ik gebruiken voor cos(x) - sin(x) ? Ik ken daar geen standaard formule voor
Dat zie ik niet staan!
Naar welk antwoord zoek je nu?
Ik bedoelde wat tussen de haken staat (2cos^2(x) - sin^2(x))
Volgens het antwoordenblad is de noemer: 1-sin(2x)
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 08 mar 2017, 15:05
Westerwolde schreef:Volgens het antwoordenblad is de noemer: 1-sin(2x)
Dat klopt niet! Kijk je nu naar de afgeleide van deze post?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 08 mar 2017, 15:16
SafeX schreef:Westerwolde schreef:Volgens het antwoordenblad is de noemer: 1-sin(2x)
Dat klopt niet! Kijk je nu naar de afgeleide van deze post?
Excuses ik haal deze post door elkaar met mijn andere post.
De afgeleide volgens het antwoordenboek: sin(x)(2-3sin2(x))
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 08 mar 2017, 16:41
Westerwolde schreef:De afgeleide volgens het antwoordenboek: sin(x)(2-3sin2(x))
Dat zal er niet staan: sin(x)(2-3sin^2(x))
En klopt dat nu met wat jij hebt gevonden
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Bericht
door Westerwolde » 09 mar 2017, 07:06
SafeX schreef:Westerwolde schreef:De afgeleide volgens het antwoordenboek: sin(x)(2-3sin2(x))
Dat zal er niet staan: sin(x)(2-3sin^2(x))
En klopt dat nu met wat jij hebt gevonden
Wat zal volgens jou het antwoord moeten zijn?
Wat kan ik verder nog doen met onderstaande?
f'(x) = sin(x) (2cos^2(x) - sin^2(x))
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 09 mar 2017, 11:32
SafeX schreef:
f'(x) = sin(x) (2cos^2(x) - sin^2(x))
Dit is jouw antwoord en dat is goed. Het antwoord in de antwoordenlijst is ook goed. Kan je dat laten zien, doe iig een poging.

