#4 afgeleide goniometrische functie
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
#4 afgeleide goniometrische functie
Hallo,
Ik heb een vraagje over de onderstaande goniometrische functie , hiervan moet ik de afgeleide berekenen.
f(x)= cos(x)+sin(x) / cos(x)-sin(x)
Mijn vraag is; moet ik de teller en noemer als een term zien, of elk als twee termen?
Ik heb een vraagje over de onderstaande goniometrische functie , hiervan moet ik de afgeleide berekenen.
f(x)= cos(x)+sin(x) / cos(x)-sin(x)
Mijn vraag is; moet ik de teller en noemer als een term zien, of elk als twee termen?
Re: #4 afgeleide goniometrische functie
Al eerder opgemerkt dat deze notatie fout is! Waarom gebruik jeWesterwolde schreef: f(x)= cos(x)+sin(x) / cos(x)-sin(x)
f(x)= cos(x)+tan(x)-sin(x). Bedoel je dat?
Verder begrijp ik je vraag niet, stel dat je teller en noemer als een term ziet, wat is dan het gevolg voor f'(x)?
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: #4 afgeleide goniometrische functie
SafeX schreef:Al eerder opgemerkt dat deze notatie fout is! Waarom gebruik je niet? Met deze notatie staat er:Westerwolde schreef: f(x)= cos(x)+sin(x) / cos(x)-sin(x)
f(x)= cos(x)+tan(x)-sin(x). Bedoel je dat?
Verder begrijp ik je vraag niet, stel dat je teller en noemer als een term ziet, wat is dan het gevolg voor f'(x)?
cos(x)+sin(x) staat boven de btreukstreep en
cos(x)-sin(x) staat onder de breukstreep
Re: #4 afgeleide goniometrische functie
Het gaat er natuurlijk niet om of ik het kan begrijpen, maar wat jij opschrijft moet juist zijn.Westerwolde schreef:= \frac{cos(x)+sin(x)}{cos(x)-sin(x)})
Met
Bekijk ook de [Equation Editor] (zie hierboven) misschien is dat gemakkelijker.
En nu je vraag ...
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: #4 afgeleide goniometrische functie
Het gaat er natuurlijk niet om of ik het kan begrijpen, maar wat jij opschrijft moet juist zijn.
Met moet je ook de LaTex-code gebruiken anders heeft het geen functie. Bekijk de vorm hierboven en zoek ook op internet naar LaTex-code.
Bekijk ook de (zie hierboven) misschien is dat gemakkelijker.
En nu je vraag ...[/quote]
Kan ik deze termen zo in de formule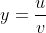 stoppen ?
stoppen ?
Met moet je ook de LaTex-code gebruiken anders heeft het geen functie. Bekijk de vorm hierboven en zoek ook op internet naar LaTex-code.
Bekijk ook de (zie hierboven) misschien is dat gemakkelijker.
En nu je vraag ...[/quote]
Kan ik deze termen zo in de formule
Re: #4 afgeleide goniometrische functie
Natuurlijk. Kijk naar:
Westerwolde schreef: Ik heb op onderstaande manier de afgeleide van een goniometrische functie bepaald :
f(x)= [1-2sin(x)] / [1+2cos(x)]
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: #4 afgeleide goniometrische functie
SafeX schreef:Natuurlijk. Kijk naar:
Westerwolde schreef: Ik heb op onderstaande manier de afgeleide van een goniometrische functie bepaald :
f(x)= [1-2sin(x)] / [1+2cos(x)]
Ja klopt, maar daar had ik alleen een sin(x) in de noemer/teller, nu heb ik cos(x) en sin(x) noemer/teller.
Ik dacht misschien moet ik dan van te voren nog een 'bewerking' uitvoeren
Re: #4 afgeleide goniometrische functie
Niemand die je daarvan kan weerhouden, maar waarom doe je het gewoon niet ...
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: #4 afgeleide goniometrische functie
SafeX schreef:Niemand die je daarvan kan weerhouden, maar waarom doe je het gewoon niet ...
Nouja het probleem is dat ik niet weet wat ik met
Re: #4 afgeleide goniometrische functie
Deze vraag is niet duidelijk, welke formule pas je toe als y=u/v, wat zijn dan u en v?Westerwolde schreef:SafeX schreef:Niemand die je daarvan kan weerhouden, maar waarom doe je het gewoon niet ...
Nouja het probleem is dat ik niet weet wat ik metaan moet..
-
Westerwolde
- Vergevorderde

- Berichten: 363
- Lid geworden op: 11 mar 2015, 13:26
Re: #4 afgeleide goniometrische functie
SafeX schreef:Deze vraag is niet duidelijk, welke formule pas je toe als y=u/v, wat zijn dan u en v?Westerwolde schreef:SafeX schreef:Niemand die je daarvan kan weerhouden, maar waarom doe je het gewoon niet ...
Nouja het probleem is dat ik niet weet wat ik metaan moet..
Ik pas de formule
Kan ik voor u aannemen :
en kan ik voor v aannemen :
Re: #4 afgeleide goniometrische functie
Dat lijkt mij de enige mogelijkheid.
