Ik was zojuist bezig met algebra en kwam op een contradictie die ik niet geheel kan plaatsen.
De vergelijking is gegeven als:
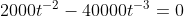
Nu snap ik dat het het makkelijkst is om deze op te lossen door beide kanten te vermenigvuldigen met
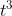
zodat ik vindt:
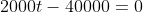
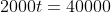
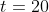
Maar ik dacht later: in principe kan ik de vergelijking ook herschrijven tot:
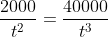
En via kruiselings vermenigvuldigen dan uitkomen op:
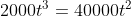
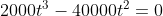
=0)
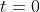
of
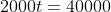
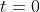
of
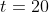
Nu is mijn probleem dat ik via deze route ook
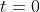
vind, maar in mijn originele vergelijking levert dit een deling door 0 op wat ongedefinieerd is; maar als ik het probleem gekregen had zoals ik het herschreef zou ik wel wegkomen met de oplossing
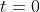
. Hoe moet ik dit plaatsen, want veel problemen die ik krijg en oplos als
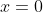
zou ik kunnen herschrijven naar een

in de noemer. Is het simpelweg niet valide om een probleem zo te herschrijven? Of mag
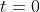
in dit geval wel goed gerekend worden?

