Matrix
Re: Matrix
Wat bedoel je?
Re: Matrix
Ik moet deze twee opgaven kunnen maken voor mijn eindexamen maar ik heb geen idee hoe je ze kan oplossen.
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Matrix
Ben je bekend met de bewijstechniek volledige inductie?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Matrix
Nee staat niet vermeld in het handboek
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Matrix
Het idee is als volgt: om een uitspraak over de natuurlijke getallen te bewijzen laat je eerst zien dat de uitspraak juist isBloedworst13 schreef:Nee staat niet vermeld in het handboek
voor n = 1. Vervolgens veronderstel je dat de uitspraak juist is voor n = k (dit heet de inductiehypothese) en met behulp daarvan toon je de juistheid voor n = k+1 aan. Uit het gegeven dat de uitspraak juist is voor n = 1 en uit het gegeven dat de juistheid voor n = k+1 uit de juistheid voor n = k volgt, volgt de juistheid van de uitspraak voor alle natuurlijke getallen n.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Matrix
Superbedankt! Ik zal op internet nog wat zoeken over die inductiemethode 
Re: Matrix
Ik snap nu wel hoe ik tot de oplossing kan komen, maar hoe bewijs je dat het klopt voor k+1?
http://imgur.com/3XZ8S19
Ik kom tot hier maar ik heb het gevoel dat ik iets fout doe
http://imgur.com/3XZ8S19
Ik kom tot hier maar ik heb het gevoel dat ik iets fout doe
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Matrix
Bedenk dat 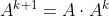 .
.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Matrix
Is het dan de bedoeling de onbekenden in de rechtermatrix weg te werken?
Ik voel me echt dom
Ik voel me echt dom
Re: Matrix
We moeten bewijzen (voor alle positieve gehele n):
\\ 0 & 2 & 4n\\ 0 & 0 & 2 \end{bmatrix})
(dus bewijzen dat links gelijk is aan rechts)
[1] Basisstap:
Voor n=1 heb je dat al aangetoond, maar veel docenten hebben het liever net iets uitgebreider, bijvoorbeeld:
\\ 0 & 2 & 4\cdot1\\ 0 & 0 & 2 \end{bmatrix})
Op deze manier zie je wat je gedaan hebt: voor n aan beide kanten 1 ingevuld, en aangetoond dat de uitkomst hetzelfde is (midden) voor beide kanten.
[2] Inductie-stap:
Stel de stelling is waar voor n = k, dan geldt voor n = k + 1 voor het linker lid (voor n vullen we nu in: k+1 ):
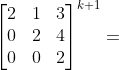
(gebruik wat arno hierboven gezegd heeft:)
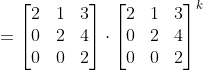
en nu gebruiken we de inductie-aanname (= de veronderstelling dat onze stelling klopt voor n = k):
\\ 0 & 2 & 4k\\ 0 & 0 & 2 \end{bmatrix} = ...)
Werk dit matrix-product uit.
Tenslotte moeten we aantonen dat het resultaat daarvan gelijk is aan het rechter lid voor n = k + 1, dus gelijk aan ( voor n weer (k+1) invullen):
-1} \cdot \begin{bmatrix} 2 & (k+1) & (k+1)((k+1)+2)\\ 0 & 2 & 4(k+1)\\ 0 & 0 & 2 \end{bmatrix})
Kom je zo verder?
(dus bewijzen dat links gelijk is aan rechts)
[1] Basisstap:
Voor n=1 heb je dat al aangetoond, maar veel docenten hebben het liever net iets uitgebreider, bijvoorbeeld:
Op deze manier zie je wat je gedaan hebt: voor n aan beide kanten 1 ingevuld, en aangetoond dat de uitkomst hetzelfde is (midden) voor beide kanten.
[2] Inductie-stap:
Stel de stelling is waar voor n = k, dan geldt voor n = k + 1 voor het linker lid (voor n vullen we nu in: k+1 ):
(gebruik wat arno hierboven gezegd heeft:)
en nu gebruiken we de inductie-aanname (= de veronderstelling dat onze stelling klopt voor n = k):
Werk dit matrix-product uit.
Tenslotte moeten we aantonen dat het resultaat daarvan gelijk is aan het rechter lid voor n = k + 1, dus gelijk aan ( voor n weer (k+1) invullen):
Kom je zo verder?
Re: Matrix
Er is nog 1 ding dat ik niet snap, wat doe je met de 2 voor elke matrix? Ze hebben beiden een andere exponent dus hoe kan je ze uitwerken?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Matrix
Als je een matrix met een bepaald getal vermenigvuldigt wordt ieder element in de matrix met dat getal vermenigvuldigd. Kijk nu eens of je aan de hand hiervan het gevraagde bewijs weet te leveren.Bloedworst13 schreef:Er is nog 1 ding dat ik niet snap, wat doe je met de 2 voor elke matrix? Ze hebben beiden een andere exponent dus hoe kan je ze uitwerken?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Matrix
JAAA ik heb de oplossing gevonden, na 3 dagen sukkelen. Echt superbedankt allemaal, ik had het niet zelf gekund.
Re: Matrix
Nog een vraag over opdracht 19 uit de eerste link die ik stuurde. Is het de bedoeling om eerst a en b in functie van a b en n te bepalen voor je de gelijkheid bewijst? Ik snap nu al dat ik inductie moet gebruiken maar ik snap de rest nog niet echt

