Goedenavond allen,
Kan iemand mij helpen?
Ik zit een beetje vast wat betreft functies met parameters. De gegeven functie is:
fc(x) = 0,5x^4 - cx^2 + c
De opgave is:
Voor welke waarden van c raakt de grafiek van fc de x-as?
Vanaf hier wordt het voor mij een beetje vaag maar dit is wat ik doe:
functie fc(x) = 0,5x^4 - cx^2 + c raakt x-as ofwel functie y(x) = 0x <-"is die x in dit geval nodig?"
snijpunten bereken:
fc(x) = y(x)
0,5x^4 - cx^2 + c = 0x
0,5x^4 - cx^2 + c - 0x = 0
0,5x^4 - cx^2 + c = 0
Omdat het gaat om de x-as "raken" wil ik de discriminant D = 0 uitrekenen.
Hiervoor noteer ik:
a = 0,5
b = -c
c = c
Vervolgens invullen voor D = b^2 - 4ac geeft D = (-c)^2 - 4(0,5)(c) = c^2 - 2c
Omdat je D = 0 wilt berekenen wordt het: c^2 - 2c = 0 = c(c - 2)
c = 0 of c = 2
In het antwoordboek staat c = 2 , dus ofwel ik heb het gedeeltelijk goed of ik heb toevallig hetzelfde antwoord gekregen met een verkeerde benadering. Mijn vraag aan jullie of ik zo een beetje in de goede richting zit?
Alvast bedankt voor het lezen!
functie met parameters
Re: functie met parameters
Je antwoord klopt. Ga dit na door de grafieken van beide functies te tekenen.
Je behandelt deze vraag door een discriminant uit te rekenen, maar deze functie is van de vierde graad. Kan je dit toelichten?
Je behandelt deze vraag door een discriminant uit te rekenen, maar deze functie is van de vierde graad. Kan je dit toelichten?
Re: functie met parameters
Bedankt voor de reactie. Ik gebruik de discriminant omdat ik 1 oplossing wil vinden voor de vergelijking fc(x) = y(x).
Of kan ik hier beter de afgeleide voor gebruiken? Omdat je fc(x) = 0 wil weten maar ook f'c(x) = 0
Of kan ik hier beter de afgeleide voor gebruiken? Omdat je fc(x) = 0 wil weten maar ook f'c(x) = 0
Re: functie met parameters
De discriminant geldt voor een kwadratische verg, maar dit is een verg van de vierde graad.
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: functie met parameters
Algemeen geldt het volgende: de grafieken van f en g raken elkaar als f(x) = g(x) en f'(x) = g'(x).
Indien g de constante functie g(x) = 0 voorstelt geeft dit de voorwaarde voor het raken van de grafiek van f aan de x-as.
Indien g de constante functie g(x) = 0 voorstelt geeft dit de voorwaarde voor het raken van de grafiek van f aan de x-as.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: functie met parameters
Is dit een betere methode?:
functie: = 0,5x^4 - cx^2 + c)
afgeleide: = 2x^3 - 2cx)
Voor welke waarden van c raakt de grafiek van fc de x-as?
Je wilt dan het volgende berekenen:
 = 0)
 = 0)
Beginnen met de afgeleide:
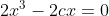
 = 0)
x = 0 of x = ±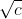
Invullen geeft = c) of
of
 = 0,5(\sqrt{c})^4 - c(\sqrt{c})^2 + c = 0)
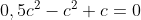
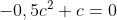
 = 0)
en dan wordt c = 0 of c = 2
hetzelfde geldt voor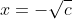
Ik krijg hiermee dezelfde oplossingen als hiervoor maar volgens mij met een betere methode.
Klopt hier nog iets van?
functie:
afgeleide:
Voor welke waarden van c raakt de grafiek van fc de x-as?
Je wilt dan het volgende berekenen:
Beginnen met de afgeleide:
x = 0 of x = ±
Invullen geeft
en dan wordt c = 0 of c = 2
hetzelfde geldt voor
Ik krijg hiermee dezelfde oplossingen als hiervoor maar volgens mij met een betere methode.
Klopt hier nog iets van?
Re: functie met parameters
Zo kan het ook.
Je eerste methode is goed maar je moet x^2 gelijkstellen aan (bv) p. Dan wordt de functie kwadratisch in p.
Je eerste methode is goed maar je moet x^2 gelijkstellen aan (bv) p. Dan wordt de functie kwadratisch in p.

