Ad blocker gedetecteerd: Onze website wordt mogelijk gemaakt door online advertenties weer te geven aan onze bezoekers. Overweeg alstublieft ons te steunen door uw advertentieblokkering op onze website uit te schakelen. of een lidmaatschap aan te kopen
Dit forum is voor het voortgezetonderwijs (of 2de/3de graad ASO), als je in de bovenbouw zit. We gaan er vanuit dat je een Grafische Rekenmachine hebt.
-
jokke_moose
- Nieuw lid

- Berichten: 13
- Lid geworden op: 13 okt 2018, 21:50
Bericht
door jokke_moose » 19 okt 2018, 11:37
Hallo,
Stel volgende vergelijking:
x + \frac{{m^{2}}}{4} = 0)
Hoe kan ik m bepalen opdat er 2 verschillende positieve wortels zijn?
Mijn werkwijze:
Discriminant =
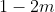
Deze moet positief zijn (aangezien er 2 oplossingen zijn):
dus:
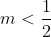
Maar hoe bepaal ik de voorwaarden voor m waarbij de wortels positief moeten zijn.
Geen idee hoe ik hier mee verder ga

-
arie
- Moderator

- Berichten: 3915
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 19 okt 2018, 15:33
Volgens de abc-formule zijn de wortels:
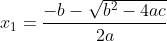
en
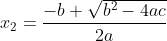
Wat zijn de wortels van jouw vergelijking?
Welke wortel is daarvan de kleinste?
Voor welke waarde(n) van m is deze kleinste wortel groter dan nul?
Kom je zo verder?
-
jokke_moose
- Nieuw lid

- Berichten: 13
- Lid geworden op: 13 okt 2018, 21:50
Bericht
door jokke_moose » 19 okt 2018, 16:16
Hallo,
Bedankt voor het snelle antwoord, maar ik ben niet zeker van wat ik verder doe.
is volgende redenering correct?
ik neem de kleinste wortel omdat deze zeker groter moet zijn dan 0 en vul in:
criteria:
 - \sqrt{1-2m}>0)
mag ik dan schrijven:
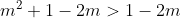
en dus uiteindelijk:

wat eigenlijk altijd ok is, vandaar mijn verwarring.
-
arie
- Moderator

- Berichten: 3915
- Lid geworden op: 09 mei 2008, 09:19
Bericht
door arie » 19 okt 2018, 16:43
jokke_moose schreef:...
 - \sqrt{1-2m}>0)
mag ik dan schrijven:
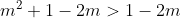
...
 - \sqrt{1-2m}>0)
ofwel
 > \sqrt{1-2m})
ofwel
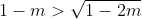
LINKS: we hadden al m < 1/2, dus 1-m > 1/2 dus niet-negatief
RECHTS: de wortel is altijd niet-negatief
dus we kunnen veilig kwadrateren zonder dat het teken omklapt.
jokke_moose schreef:...

wat eigenlijk altijd ok is, vandaar mijn verwarring.
NIET altijd: er is (precies) één waarde van m waarvoor dit NIET geldt.
Welke waarde?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Bericht
door arno » 19 okt 2018, 18:34
Ga na dat uitsluitend aan m²>0 voldaan wordt als |m|>0. Wat betekent dit voor m?
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
-
SafeX
- Moderator

- Berichten: 14278
- Lid geworden op: 29 dec 2005, 11:53
Bericht
door SafeX » 19 okt 2018, 22:10
Gelukkig kan het allemaal wat eenvoudiger.
m<1/2 is correct.
Bedenk nu dat, als de opl aangegeven worden met x1 en x2, er moet gelden:
x1+x2=
x1*x2=
Kan je dit aanvullen zonder rekenwerk?
Zo ja, welke eis moet je stellen aan som en product van de opl als beide pos moeten zijn?
-
jokke_moose
- Nieuw lid

- Berichten: 13
- Lid geworden op: 13 okt 2018, 21:50
Bericht
door jokke_moose » 15 nov 2018, 20:15
excuses voor het (heel) late antwoord. Inderdaad met X1+X2 en X1*X2 lukt het ook, maar dat hadden we toen nog niet gezien



