Wiskundeforum

Ik kom er niet uit Kan iemand mij helpen?



https://imgur.com/a/aRCdX4s

Alvast bedankt!

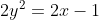
We kunnen bovenstaande formule omvormen tot de volgende vergelijking :



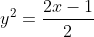
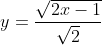
en

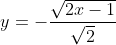
De eerste formule is de bovenste tak en de tweede tak , de gespiegelde naar onder in de X-as.
We zien nu als we voor x want in de vergelijking
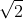
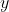
wordt gedeeld door en daardoor kan nooit een geheel getal zijn want
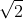
is een irrationaal getal.

Nu moeten we ook nog bewijzen als y



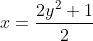
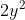
is altijd een even getal en doe daar +1 en dan bekom je altijd een oneven getal.
En als je dit oneven getal in de teller deelt door 2 bekom je nooit een geheel getal.

Dus x en y van deze grafiek zal nooit door roosterpunten gaan waarvan x en y een geheel getal zijn.

Het antwoord van steinbach is volledig. Je kan je argument wiskundig "mooier" formuleren door het bijvoorbeeld expliciet op te schrijven als een bewijs uit het ongerijmde:

Te bewijzen: \(V \cap N = \emptyset \)
Bewijs: Veronderstel dat \(V \cap N \neq \emptyset \), i.e dan bestaat er een \(x \in N\) en \(y \in N\) zodanig dat \(2x - 1 = 2y^2\) etc... (gebruik dan het argument van steinbach wat duidelijk to een contradictie leidt).

Een nog korter bewijs:

Voor alle \(x \in \mathbb{Z}\) is \(2x-1\) oneven
Voor alle \(y \in \mathbb{Z}\) is \(2y^2\) even
En een oneven getal kan nooit gelijk zijn aan een even getal.


PS: TIP: als je op dit forum een plaatje wilt tonen, gebruik dan de link naar het .jpg bestand van dat plaatje.
(en niet de link naar de website; ik heb je oorspronkelijke post hierop aangepast).

PPS: De opgave kan ook nog wat netter:
\(V \cap \; \mathbb{Z} \times \mathbb{Z} = \emptyset\)
Immers: V is een verzameling geordende paren \((x,y) \in \mathbb{R} \times \mathbb{R}\) die voldoen aan \(2x-1=2y^2\);
als x en y bovendien geheel moeten zijn, dan moet \((x,y) \in \mathbb{Z} \times \mathbb{Z}\).

Dank voor alle reacties!