Vereenvoudigen wortel van een breuk
Vereenvoudigen wortel van een breuk
Hallo,
Ik had een vraagje ivm met het vereenvoudigen van een wortel van een breuk.
Wanneer beide wortels, vierkantswortels waren dacht ik gewoon de wortel in de noemer te vermenigvuldigen met de teller en noemer, maar dat gaat hier waarschijnlijk niet op.
De oefening is, de 4de wortel van 12 / de wortel van 20.
Iemand een idee?
Alvast bedankt !
Ik had een vraagje ivm met het vereenvoudigen van een wortel van een breuk.
Wanneer beide wortels, vierkantswortels waren dacht ik gewoon de wortel in de noemer te vermenigvuldigen met de teller en noemer, maar dat gaat hier waarschijnlijk niet op.
De oefening is, de 4de wortel van 12 / de wortel van 20.
Iemand een idee?
Alvast bedankt !
Re: Vereenvoudigen wortel van een breuk
Het kan op jouw manier:
\(\frac{\sqrt[4]{12}}{\sqrt{20}}=\frac{\sqrt[4]{12}\cdot \sqrt{20}}{\sqrt{20}\cdot \sqrt{20}}=\frac{\sqrt[4]{12}\cdot \sqrt{20}}{20}=\frac{1}{20}\cdot \sqrt[4]{12}\cdot \sqrt{20}\)
Om de wortels te kunnen samentrekken moeten ze dezelfde macht hebben.
Kan je \(\sqrt{20}\) eerst herschrijven als 4-de machts wortel?
Dus
\(\sqrt{20} = \sqrt[4]{???}\)
En kan je daarmee het product nog vereenvoudigen?
\(\frac{\sqrt[4]{12}}{\sqrt{20}}=\frac{\sqrt[4]{12}\cdot \sqrt{20}}{\sqrt{20}\cdot \sqrt{20}}=\frac{\sqrt[4]{12}\cdot \sqrt{20}}{20}=\frac{1}{20}\cdot \sqrt[4]{12}\cdot \sqrt{20}\)
Om de wortels te kunnen samentrekken moeten ze dezelfde macht hebben.
Kan je \(\sqrt{20}\) eerst herschrijven als 4-de machts wortel?
Dus
\(\sqrt{20} = \sqrt[4]{???}\)
En kan je daarmee het product nog vereenvoudigen?
Re: Vereenvoudigen wortel van een breuk
Bedankt,
Oke top het eerste deel begrijp ik maar niet het omvormen van de vierkantswortel van 20 naar een vierdegraadswortel.
Is dat dan geen heel groot kommagetal?
Oke top het eerste deel begrijp ik maar niet het omvormen van de vierkantswortel van 20 naar een vierdegraadswortel.
Is dat dan geen heel groot kommagetal?
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Vereenvoudigen wortel van een breuk
Stel 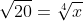 . Links en rechts alles tot de vierde macht verheffen levert dan:
. Links en rechts alles tot de vierde macht verheffen levert dan: ^4=20^2=400) . Merk op dat algemeen geldt dat
. Merk op dat algemeen geldt dat 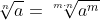 .
.
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Vereenvoudigen wortel van een breuk
Oke dan heb ik,
1/20 * vierdemachtswortel van (12*400=4 800).
Wat is de beste manier om te kijken of je dit nu kan vereenvoudigen?
1/20 * vierdemachtswortel van (12*400=4 800).
Wat is de beste manier om te kijken of je dit nu kan vereenvoudigen?
Re: Vereenvoudigen wortel van een breuk
Je kan het getal ontbinden in (priem-)factoren.
Omdat we hier al een product hebben:
4800 = 12 * 20 * 20
is het eenvoudiger (=minder rekenwerk) om deze factoren eerst individueel te ontbinden:
\(12\cdot 20 \cdot 20 = (2^2 \cdot 3) \cdot (2^2 \cdot 5) \cdot (2^2 \cdot 5) = 2^6 \cdot 3 \cdot 5^2\)
Zie je hierin een vierde macht die je buiten de vierdemachts wortel kan halen?
Omdat we hier al een product hebben:
4800 = 12 * 20 * 20
is het eenvoudiger (=minder rekenwerk) om deze factoren eerst individueel te ontbinden:
\(12\cdot 20 \cdot 20 = (2^2 \cdot 3) \cdot (2^2 \cdot 5) \cdot (2^2 \cdot 5) = 2^6 \cdot 3 \cdot 5^2\)
Zie je hierin een vierde macht die je buiten de vierdemachts wortel kan halen?
Re: Vereenvoudigen wortel van een breuk
Ik weet het niet, we hebben toch enkel een 2de en 6de macht?
Re: Vereenvoudigen wortel van een breuk
Bedenk:
\(a^{m+n} = a^m \cdot a^n\)
Voorbeeld:
\(27 = 3^3 = 3^{2+1} = 3^2 \cdot 3^1 = 9\cdot 3 \)
In ons geval zoeken we vierde machten die we af kunnen splitsen:
\(2^6 = 2^{4+2} = ...\)
\(a^{m+n} = a^m \cdot a^n\)
Voorbeeld:
\(27 = 3^3 = 3^{2+1} = 3^2 \cdot 3^1 = 9\cdot 3 \)
In ons geval zoeken we vierde machten die we af kunnen splitsen:
\(2^6 = 2^{4+2} = ...\)
Re: Vereenvoudigen wortel van een breuk
2^6 * 3 * 5^2
Dan kunnen we 2^4 afsplitsen en dan krijgen we 2^2 * 3 * 5^2 = 10^4 * 3 , correct?
Staan beide dan nu buiten de 4demachtswortel?
Dan kunnen we 2^4 afsplitsen en dan krijgen we 2^2 * 3 * 5^2 = 10^4 * 3 , correct?
Staan beide dan nu buiten de 4demachtswortel?
Re: Vereenvoudigen wortel van een breuk
Nee, we hebben hier alleen gekeken naar die 4800, en vastgesteld dat we er een factor \(2^4\) van kunnen afsplitsen.
Ofwel, terug naar ons probleem:
\(\frac{\sqrt[4]{12}}{\sqrt{20}}=\frac{1}{20}\cdot \sqrt[4]{4800}=\frac{1}{20}\cdot \sqrt[4]{2^4 \cdot 2^2 \cdot 3 \cdot 5^2} \)
en nu kunnen we wat onder die vierdemachts wortel staat splitsen in een deel met zuivere 4e machten (bij ons alleen \(2^4\)), en een deel waar geen vierde machten meer in zitten:
\(\frac{1}{20}\cdot \sqrt[4]{2^4 \cdot 2^2 \cdot 3 \cdot 5^2} = \frac{1}{20}\cdot \sqrt[4]{2^4} \cdot \sqrt[4]{2^2 \cdot 3 \cdot 5^2} \)
Het deel met vierde machten kunnen we nu vereenvoudigen, het deel zonder vierde machten niet meer (dit laatste kunnen we laten staan of terug omzetten naar een getal, hier \(2^2 \cdot 3 \cdot 5^2 = 300\)).
Kan je dit nu verder vereenvoudigen,?
Ofwel: wat komt hier op de 3 puntjes te staan?:
\( = \frac{1}{20}\cdot \; \dots \; \cdot \sqrt[4]{300} \)
En wat wordt vervolgens het eindantwoord?
Ofwel, terug naar ons probleem:
\(\frac{\sqrt[4]{12}}{\sqrt{20}}=\frac{1}{20}\cdot \sqrt[4]{4800}=\frac{1}{20}\cdot \sqrt[4]{2^4 \cdot 2^2 \cdot 3 \cdot 5^2} \)
en nu kunnen we wat onder die vierdemachts wortel staat splitsen in een deel met zuivere 4e machten (bij ons alleen \(2^4\)), en een deel waar geen vierde machten meer in zitten:
\(\frac{1}{20}\cdot \sqrt[4]{2^4 \cdot 2^2 \cdot 3 \cdot 5^2} = \frac{1}{20}\cdot \sqrt[4]{2^4} \cdot \sqrt[4]{2^2 \cdot 3 \cdot 5^2} \)
Het deel met vierde machten kunnen we nu vereenvoudigen, het deel zonder vierde machten niet meer (dit laatste kunnen we laten staan of terug omzetten naar een getal, hier \(2^2 \cdot 3 \cdot 5^2 = 300\)).
Kan je dit nu verder vereenvoudigen,?
Ofwel: wat komt hier op de 3 puntjes te staan?:
\( = \frac{1}{20}\cdot \; \dots \; \cdot \sqrt[4]{300} \)
En wat wordt vervolgens het eindantwoord?
Re: Vereenvoudigen wortel van een breuk
Dus dan is het,
1/20 * 2 * 4demachtswortel van 300
= 1/10 * 4demachtswortel van 300 ?
1/20 * 2 * 4demachtswortel van 300
= 1/10 * 4demachtswortel van 300 ?
Re: Vereenvoudigen wortel van een breuk
Klopt.
(voor alle zekerheid kan je het ook nog controleren met je rekenmachine:
\(\frac{\sqrt[4]{12}}{\sqrt{20}}\approx 0.416179145...\)
en
\(\frac{1}{10}\sqrt[4]{300} \approx 0.416179145...\)
allebei hetzelfde, zoals verwacht)
(voor alle zekerheid kan je het ook nog controleren met je rekenmachine:
\(\frac{\sqrt[4]{12}}{\sqrt{20}}\approx 0.416179145...\)
en
\(\frac{1}{10}\sqrt[4]{300} \approx 0.416179145...\)
allebei hetzelfde, zoals verwacht)
Re: Vereenvoudigen wortel van een breuk
Oke bedankt, en mocht de oefening nu zijn:
4*vierkantswortel (12) / vierkantswortel (20)
= 4* vierkantswortel (12*20=240) / 20
= 1/20 * 4 * vierkantswortel (240)
= maar dan zit ik opnieuw vast..
4*vierkantswortel (12) / vierkantswortel (20)
= 4* vierkantswortel (12*20=240) / 20
= 1/20 * 4 * vierkantswortel (240)
= maar dan zit ik opnieuw vast..
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Vereenvoudigen wortel van een breuk
Merk om te beginnen op dat √12 = 2√3 en √20 = 2√5, dus 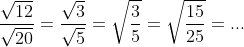 , dus
, dus 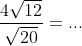
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Vereenvoudigen wortel van een breuk
Sorry ik volg even niet,
Dus de 4* vierkantswortel (12) = vierkantswortel (3)
en vierkantswortel (20) = vierkantswortel (5) ?
Dus de 4* vierkantswortel (12) = vierkantswortel (3)
en vierkantswortel (20) = vierkantswortel (5) ?

