Zie bijgevoegde oefening.
https://imgur.com/a/gtv4wFL
Bij deel 4) berekening van de Inhoud kom ik niet aan het resultaat van in het leerboek.
Het voorschrift in deel 2) welke de oppervlakte beschrijft is \(f(x)=-\frac{1}{2}x^{2}+5x\)
Om de inhoud te berekenen van de cilinder die je bekomt door de rechthoek OAPB om de
y-as te wentelen ging ik als volgt te werk.
\(g(x)= 2\Pi x.f(x)\)
\(g(x)=(-\frac{1}{2}x^{2}+5x).2\Pi .x\)
\(g(x)=-\Pi x^{3}+10\Pi x^{2}\)
In het boek komt men een andere oplossing uit ???
Klopt dit of redeneer ik ergens fout ?
Inhoud
-
arno
- Vergevorderde

- Berichten: 1923
- Lid geworden op: 25 dec 2008, 16:28
- Locatie: Beek en Donk, Noord-Brabant
Re: Inhoud
Ga nog eens na wat de primitieve functie, ofwel stamfunctie, is van -½x+5. Stel P ligt op de rechte y = -½x+5, dan weet je in ieder geval dat P weer te geven is als P(x,-½x+5). Je weet dan ook voor welke x P boven de x-as ligt. Bedenk nu verder dat de cilinder die je krijgt de straal AP en de hoogte OA heeft. Je kunt de inhoud van de cilinder dus uitdrukken in x.
Aanvullende opmerking: de kleine letter π heeft in de wiskunde de betekenis van het irrationale getal 3,14159..., terwijl de hoofdletter Π gebruikt wordt om een product weer te geven, bijvoorbeeld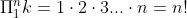 .
.
Aanvullende opmerking: de kleine letter π heeft in de wiskunde de betekenis van het irrationale getal 3,14159..., terwijl de hoofdletter Π gebruikt wordt om een product weer te geven, bijvoorbeeld
"Mathematics is a gigantic intellectual construction, very difficult, if not impossible, to view in its entirety." Armand Borel
Re: Inhoud
Dag arno ,
Als ik jouw redenering toepas dan kom ik tot volgend resultaat :
\(V_{cilinder}=\pi r^{2}h\)
\(g(x)=\pi x^{2}(-\frac{1}{2}x+5)\)
\(g(x)=-\frac{\pi }{2}x^{3}+5\pi x^{2}\)
En dat klopt met het resultaat achteraan in het leerboek.
Ik heb intussen ook het kleine symbool voor pi gevonden.
Hartelijk dank arno.
Als ik jouw redenering toepas dan kom ik tot volgend resultaat :
\(V_{cilinder}=\pi r^{2}h\)
\(g(x)=\pi x^{2}(-\frac{1}{2}x+5)\)
\(g(x)=-\frac{\pi }{2}x^{3}+5\pi x^{2}\)
En dat klopt met het resultaat achteraan in het leerboek.
Ik heb intussen ook het kleine symbool voor pi gevonden.
Hartelijk dank arno.